Bernoulli egyenlet képlete. Iskolai enciklopédia

Időpontja: 2009-10-20

Egy valódi folyadék két, 1-1 és 2-2 áramlási szakaszára (1. ábra) egyenletesen, egyenletesen változó mozgással a Bernoulli-egyenlet a következő:

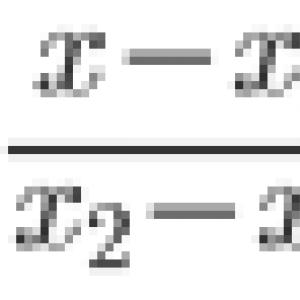
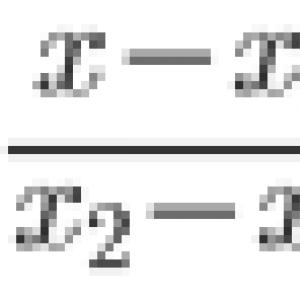
z 1 + p 1 /γ + α 1 υ 1 2 /(2g) = z 2 + p 2 /γ + α 2 υ 2 2 /(2g) + Σh p (1)

Ahol z- ordináta, amely meghatározza a kiválasztott szakasz középpontjának helyzetének magasságát egy tetszőleges vízszintes összehasonlító sík felett 0-0; p/γ- piezometrikus magasság; z + p/γ = H p- hidrosztatikus fej; αυ 2 /(2g) = hv- sebességmagasság vagy sebességnyomás; α - Coriolis-együttható, amely figyelembe veszi a sebességek egyenetlen eloszlását az áramlás élő keresztmetszetében.

Három kifejezés összege:

z + p/γ + αυ 2 /(2g) = H

teljes nyomás van; Σh p- nyomásveszteség a kiválasztott áramlási szakaszok között. Az (1) kifejezés helyett a következőket írhatja:

H 1 = H 2 + Σh p

Az (1) képletben szereplő Bernoulli-egyenlet minden tagjának lineáris dimenziója van, és energia értelemben a folyadék fajlagos energiája, azaz a folyadék egységnyi tömegére jutó energia.

Így, zÉs p/γ- helyzet és nyomás fajlagos potenciális energiája;
z + p/γ- a folyadék fajlagos potenciális energiája;
αυ 2 /(2g)- fajlagos kinetikus energia, egy adott szakaszon az átlagos áramlási sebességben kifejezve. Mindhárom kifejezés összege z + p/γ + αυ 2 /(2g) = H a folyadék fajlagos mechanikai energiájának teljes tartalékát jelenti egy adott áramlási szakaszban;
Σh p- az áramlási szakaszok közötti folyadékmozgással szembeni ellenállás leküzdésére és hőenergiává alakítására fordított fajlagos mechanikai energia, amely a következő kifejezésekből áll:

Σh p = Σh dl + Σh helyek

Ahol Σh érte- energiaveszteség (nyomás) a hossz menti súrlódás miatt; Σh helyek- helyi energia (nyomás) veszteségek.

Ha az (1) egyenletet megszorozzuk γ-val, a következőt kapjuk:

γz 1 + p 1 + γα 1 υ 1 2 /(2g) = γz 2 + p 2 + γα 2 υ 2 2 /(2g) + γΣh p (2)

A (2) egyenlet feltételeinek a nyomás dimenziója van, és az egységnyi térfogatra jutó energiát jelentik.

Ha az (1) egyenletet megszorozzuk g-vel, akkor azt kapjuk

gz 1 + p 1 /ρ + α 1 υ 1 2 / 2 = gz 2 + p 2 /ρ + α 2 υ 2 2 / 2 + gΣh p (3)

A (3) egyenlet tagjai m 2 /s 2 méretűek, és az egységnyi tömegre jutó energiát jelentik.

1. KÉP

Az 1. ábra a Bernoulli-egyenlet diagramját mutatja valós folyadékáramlásra. Itt 0-0 - összehasonlító sík; N-N- a kezdeti nyomás síkja; N-N- nyomóvezeték vagy teljes fajlagos energia vonal. Hosszegységenkénti esése a hidraulikus lejtőt jelenti J; R-R- piezometrikus vonal, vagy fajlagos potenciális energia vonal. Az egységnyi hosszra eső esése a piezometrikus meredekséget jelenti J p.

Mivel a teljes fajlagos energiatartalék az áramlás mentén folyamatosan csökken, a vonal N-N mindig lefelé, és a hidraulikus lejtő mindig pozitív ( J>0). A piezometrikus vonal lehet lefelé és felfelé is (utóbbi táguló szakaszokon fordul elő, amikor az átlagos áramlási sebesség csökken), ezért a piezometrikus meredekség pozitív is lehet ( J>0), és negatív ( J).

Azokon a területeken, ahol egyenletes a folyadékmozgás, ahol csak a hosszirányú súrlódásból eredő nyomásveszteség, vonalak N-NÉs R-R egymással párhuzamos egyeneseket képviselnek tehát J = J p = h dl / L. Ebben az esetben a nyomásveszteség a hidrosztatikus magasságok különbségével határozható meg:

h dl = (z 1 + p 1 /γ) - (z 2 + p 2 /γ)

2. ÁBRA

Vízszintes áramlási szakaszokhoz ( z 1 = z 2) vagy ha az összehasonlítási síkot 0-0 az áramlási tengely mentén rajzolva ( z 1 = z 2 = 0) (2. ábra), a hossz menti súrlódás miatti nyomásveszteség közvetlenül meghatározható a piezométer leolvasási különbségéből:

h dl = (p 1 - p 2)/γ

A 3. ábra az energiavonalat mutatja N-Nés piezometrikus vonal P-P két nyitott tartályt összekötő változó keresztmetszetű csővezetékhez.

3. ÁBRA

Forrás: Vilner Ya.M. Hidraulika, hidraulikus gépek és hidraulikus hajtások kézikönyve.

Megjegyzések ehhez a cikkhez!!

Mi a jó? Úgy tűnik, megértett valamit ebből! Az emberek már hülyék lettek, és mindezt még 1697-ben fejlesztették ki! Ez most senkinek nem jutott volna eszébe!

Beköltözöm, de lassan, annyi érdekes dolog

Bernoulli egyenlete a 23. században is érvényben marad

Mi köze Bernoulli törvényének a repüléshez? Kiderül, hogy ez a legközvetlenebb. Segítségével megmagyarázható a repülőgép szárnyának emelőereje és más aerodinamikai erők kialakulása.

Bernoulli törvénye

E törvény szerzője az Svájci egyetemes fizikus, szerelő és matematikus. Daniel Bernoulli a híres svájci matematikus, Johann Bernoulli fia. BAN BEN 1838-ban publikálta „Hidrodinamika” tudományos alapműve, amelyben levezette híres törvényét.

Azt kell mondani, hogy akkoriban az aerodinamika mint tudomány még nem létezett. Bernoulli törvénye pedig az ideális folyadék áramlási sebességének a nyomástól való függését írja le. De a huszadik század elején a repülés kezdett kialakulni. És itt nagyon jól jött Bernoulli törvénye. Hiszen ha a légáramot összenyomhatatlan folyadéknak tekintjük, akkor ez a törvény a légáramlásokra is érvényes. Segítségével meg tudták érteni, hogyan lehet a levegőnél nehezebb repülőgépet a levegőbe emelni. Ez az aerodinamika legfontosabb törvénye, hiszen kapcsolatot teremt a légmozgás sebessége és a benne ható nyomás között, ami segít a repülőgépre ható erők számításában.

Bernoulli törvénye az energiamegmaradás törvényének következménye az ideális és összenyomhatatlan folyadék álló áramlása .

Az aerodinamikában a levegőt úgy tekintik összenyomhatatlan folyadék , azaz olyan közeg, amelynek sűrűsége nem változik a nyomás változásával. A helyhez kötött Olyan áramlást tekintünk, amelyben a részecskék időben invariáns pályákon mozognak, amelyeket áramvonalaknak nevezünk. Az ilyen áramlásokban nem képződnek örvények.

A Bernoulli-törvény lényegének megértéséhez ismerkedjünk meg a sugárfolytonossági egyenlettel.

Fúvóka folytonossági egyenlete

Ebből egyértelmű, hogy minél nagyobb a folyadék áramlási sebessége (aerodinamikában pedig a légáramlás sebessége), annál kisebb a nyomás, és fordítva.

A Bernoulli-effektus a kandalló mellett ülve figyelhető meg. Erős széllökések esetén a légáramlás sebessége nő, a nyomás csökken. A helyiség légnyomása magasabb. És a lángok felrohannak a kéményen.

Bernoulli törvénye és repülése

Ennek a törvénynek a felhasználásával nagyon egyszerű elmagyarázni, hogyan történik az emelkedés a levegőnél nehezebb repülőgépeknél.

Repülés közben úgy tűnik, hogy a repülőgép szárnya két részre vágja a légáramlást. Az egyik rész a szárny felső felületén, a másik az alsó felületén folyik. A szárny alakja olyan, hogy a felső áramlásnak hosszabb utat kell megtennie ahhoz, hogy egy ponton kapcsolódjon az alsóhoz. Ez azt jelenti, hogy nagyobb sebességgel halad. És mivel a sebesség nagyobb, akkor a nyomás a szárny felső felülete felett kisebb, mint az alsó alatt. Ezeknek a nyomásoknak a különbsége miatt a szárny emelőereje keletkezik.

Ahogy a repülőgép emelkedik a magasságban, a nyomáskülönbség növekszik, ami azt jelenti, hogy az emelőerő is növekszik, ami lehetővé teszi, hogy a gép felfelé emelkedjen.

Azonnal tisztázzuk, hogy a fent leírt törvények akkor érvényesek, ha a légáramlás sebessége nem haladja meg a hangsebességet (340 m/s-ig). Hiszen a levegőt összenyomhatatlan folyadéknak tekintettük. De kiderül, hogy a hangsebesség feletti sebességnél a légáramlás másként viselkedik. A levegő összenyomhatósága már nem elhanyagolható. És ilyen körülmények között a levegő, mint minden gáz, megpróbál kitágulni, és nagyobb térfogatot foglal el. Jelentős nyomásesések vagy lökéshullámok jelennek meg. És maga a légáramlás nem szűkül, hanem éppen ellenkezőleg, kitágul. A hangsebességhez közeli vagy azt meghaladó sebességű légáramlások mozgásának problémájával foglalkozik gázdinamika , amely az aerodinamika folytatásaként keletkezett.

Az aerodinamikai törvények felhasználásával az elméleti aerodinamika lehetővé teszi a repülőgépre ható aerodinamikai erők számítását. Ezeknek a számításoknak a helyességét pedig úgy ellenőrizzük, hogy a megépített modellt speciális kísérleti berendezéseken teszteljük, amelyek ún. szélcsatornák . Ezek a berendezések lehetővé teszik az erők nagyságának mérését speciális műszerekkel.

Az aerodinamikai modellekre ható erők vizsgálata mellett aerodinamikai mérésekkel vizsgálják a modell körül áramló levegő sebességének, sűrűségének és hőmérsékletének eloszlását.

A Bernoulli-egyenletet a folyadékmechanika egyik alaptörvényének tekintik, amely kapcsolatot teremt a folyadékáramlás nyomása és a hidraulikus rendszerekben való mozgási sebessége között: az áramlási sebesség növekedésével a nyomásnak csökkennie kell. . Segít megmagyarázni számos hidrodinamikai hatást. Nézzünk néhány közismertet. A folyadék felemelése és permetezése a permetezőpalackban (1. ábra) a folyadékot tartalmazó edénybe süllyesztett csövön nagy sebességgel áthaladó levegőáram csökkentett nyomása miatt következik be. A folyadék felfelé emelkedik a légköri nyomás hatására, amely nagyobb, mint a légáram nyomása.
Egy ping-pong labda (2. ábra) folyamatosan lebeg egy függőleges légáramban, mivel a sugárban a nyomás kisebb, mint a légköri nyomás, ami a labdát a patakhoz nyomja, megakadályozva, hogy leessen.
A párhuzamos pályán haladó hajók (3. ábra) vonzódnak egymáshoz, ami számos tengeri katasztrófa okozója. Ez azzal magyarázható, hogy a hajók közötti nyomás csökken a közöttük lévő beszűkült térben a víz nagyobb sebessége miatt.
A szárny emelése (4. ábra) a nyomáskülönbség jelenléte miatt következik be p1És p2 sebességkülönbség miatt V1És V2, Amikor V1 Kevésbé V2, mivel a szárny felett elhelyezkedő levegőrészecskék nagyobb utat tesznek meg, mielőtt a szárny végén találkoznának, mint az alatta elhelyezkedő részecskék.
Ha két egymáshoz érő papírlap közé fúj (5. ábra), azok nem válnak el egymástól, ahogyan ennek megtörténnie kellene, hanem éppen ellenkezőleg, egymáshoz nyomódnak.
Így azt látjuk, hogy a Bernoulli-egyenlet széleskörű alkalmazási körrel rendelkezik számos hidrodinamikai jelenség magyarázatára. Daniel Bernoulli 1738-ban publikálta, sok évnyi gondolkodás és kutatás, keresés és kétség után. Teljesen biztos volt az általa felfedezett törvény helyességében, amely összeköti a folyadékban lévő statikus nyomást a mozgás sebességével.
Tekintsük ennek az egyenletnek a levezetését egy elemi folyadékáramra (streamline), ahogyan az minden tankönyvben megadja, egy ideális összenyomhatatlan folyadék stacionárius lamináris áramlására. A gravitációnak a folyadék mozgására gyakorolt ​​hatásának kiküszöbölésére a cső vízszintes szakaszát (6. ábra) vesszük, és az elemi áramlást vízszintesen helyezzük el.
Tekintsük egy folyadékelem mozgását, amelyet a hossz határozza meg l1. A folyadék kiválasztott részét érinti a statikus nyomás által létrehozott hajtóerő p1:
, (1)
Ahol S1- a kiválasztott folyadékszakasz bal oldalán lévő keresztmetszeti terület és a statikus nyomás által meghatározott ellenállási erő p2:
, (2)
Ahol S2- keresztmetszeti terület a telek jobb oldalán.
A folyadékelem oldalsó felületére ható nyomás a szerzők szerint merőleges az elmozdulásokra, és nem végez semmilyen munkát.
E két erő hatására a folyadék felszabadult része balról jobbra mozog. Tegyük fel, hogy kis távolságra mozog, és a hossz által meghatározott pozíciót veszi fel l2, míg a folyadékelem bal vége a D mennyiséggel fog elmozdulni l1, a jobb pedig D értékkel l2.
A mechanika törvényeinek megfelelően egy folyadékelem mozgását az fogja jellemezni, hogy a mozgási energiájának változása megegyezik a rá ható összes erő munkájával:
, (3)
Ahol m- a kiválasztott folyadékelem tömege, és - tömegközéppontjának végső és kezdeti sebessége.
A (3) kifejezés jobb oldala transzformálható, ha odafigyelünk arra, hogy a kiválasztott elem mindkét pozíciójában van egy közös rész (a 6. ábrán nincs árnyékolva), amelynek kinetikai energiája azonos lesz. Az energiának ez a része a (3) egyenletbe úgy írható be, hogy a jobb oldalon összeadjuk és kivonjuk:
(4)
Ahol mtotal- a közös rész tömege, - a közös rész tömegközéppontjának sebessége.
A zárójelben lévő kifejezések a D hosszúságú árnyékolt területek kinetikus energiáit jelentik l1és D l2, kis kiterjedésük miatt minden pontra állandó sebességgel mozognak V1És V2. Ezért a (4) egyenlet a következőképpen alakul:
, (5)
Ahol Dm1És Dm2- árnyékolt folyadékterületek tömegei.
A folyadékáramlás folytonossága miatt az árnyékolt részek térfogata és tömege egyenlő lesz:
, (6)
Ahol r- folyadék sűrűsége.
Az (5) kifejezés elosztása ezzel S1Dl1=S2Dl2, alakítsa át a következőre:
(7)
A kifejezések átrendezése után az egyenlet a következőképpen alakul:
(8)
Ez a Bernoulli-egyenlet. Mivel egy folyadékelem az áramlásban bárhol és tetszőleges hosszúságú, a Bernoulli-egyenlet a következőképpen írható fel:
, (9)
ahol p és V a statikus nyomás és a mozgás sebessége az elemi folyadékáram bármely pontján. Kifejezés rV2/ 2 dinamikus nyomásnak nevezzük.
A (9) egyenletből az következik, hogy azokon a pontokon, ahol a sebesség nagyobb, a statikus nyomás kisebb lesz, és fordítva. Hogy ez valóban így van, azt a tapasztalatok igazolják. Vegyünk példának egy Venturi csövet (7. ábra). A mérőcsövekben lévő folyadékszintek egyértelműen azt mutatják, hogy a statikus nyomás kisebb az összehúzó végén, ahol az áramlási sebesség nagyobb. Ráadásul ezt megerősítheti az a tény is, hogy a kapott eredmény, ahogyan a műben szerepel, Newton második törvényének egyenes következménye. Valóban, amikor egy folyadék széles részről egy szűkebb részre mozog, sebessége nő, és a gyorsulás a mozgás irányába irányul. És mivel a gyorsulást a bal és jobb oldali folyadékelemre ható nyomáskülönbség határozza meg, a cső széles részén a nyomásnak nagyobbnak kell lennie, mint a keskeny részén. Igaz, itt észrevehető, hogy a gyorsulást nem a nyomás, hanem az erő határozza meg, és az erő nem csak a nyomástól, hanem a keresztmetszeti területtől is függ. Ezért kisebb nyomással nagyobb erő érhető el, így a bemutatott érv nem meggyőző.
Tehát a fenti érvelésben minden logikusnak tűnik. Azonban minden hidrodinamikai hatást másként is meg lehet magyarázni. A helyzet az, hogy mindig nem ideális, hanem viszkózus folyadékkal van dolgunk, amely teljesen másként viselkedik.
Nézzük meg, mi történik a csövön átfolyó viszkózus folyadékkal (8. ábra). A folyadékáram és a cső falai, valamint magának a folyadéknak a rétegei közötti súrlódás miatt a folyadékrészecskék sebessége az áramlás ugyanazon szakaszának különböző pontjain eltérő lesz: középen a csőből maximum, a falak közelében nulla lesz. Ennek eredményeként a folyadékáramlás keresztmetszetében a sebességmezőt a következő kifejezés határozza meg:
, (10)
Ahol V- sebesség az áramlás középpontjában, r- áramsugár, R a cső sugara, és a 8. ábrán látható alakja lesz. A sebességmezővel elválaszthatatlanul kapcsolódik a kinetikus energia skaláris mezeje, amelyet a következő kifejezés jellemez:
, (11)
Ahol Edm- a felszabaduló elemi tömeg mozgási energiája dm, amelyet a következő kifejezés határoz meg:
(12)
Itt: dl- elemi hossz axiális irányban, r- folyadék sűrűsége.
Mivel a kinetikus energiatér nem egyenletes, a folyadék elemi részecskéire az áramlás középpontja felé irányuló erő hat:
(13)
Ez az erő a részecskefelület hengeres részére vonatkozott dS, amely általában az erőhöz helyezkedik el:
, (14)
meghatározza az áramlás egy adott pontjában egy adott erő hatására fellépő nyomást:
(15)
Ez a nyomás csak az elemi erőtől függ dF, tehát nyomáskülönbségnek nevezhető. A folyadék egy adott pontján a teljes nyomás a folyadék többi részecskéire ható elemi tehetetlenségi erőktől függ. Mert minden erőt dF sugárirányú irányúak és az áramlás közepe felé irányulnak, a pontban a teljes nyomást az ugyanazon a sugáron fekvő és a kérdéses ponton kívüli oldalon elhelyezkedő erők határozzák meg. Ezért a teljes nyomást a (15) kifejezés integrálásával találhatjuk meg r kezdve r előtt R:
(16)
Itt a mínusz jel jelzi a tömörítés irányát (a szakasz közepe felé).
Az eredmény meglepő volt, mivel ez a kifejezés hasonló a kinetikus energia (11) kifejezéséhez, amely az elemi tömeg térfogatára vonatkozik. dm:
, (17)
azok. az össznyomás a mozgási energia sűrűsége egy bizonyos elemi térfogatban a kérdéses pont közelében.
A (16) kifejezésből az következik, hogy az áramlási tengelyen (at r=0) a nyomás maximális lesz, és a határán (at r=R) egyenlő lesz nullával.
Radiális erők hatására az áramlás a tengelye felé összenyomódik, aminek következtében a csőfalakra nehezedő nyomás csökken, pl. negatív nyomás jelenik meg, melynek értéke a (16) kifejezés radiális átlagaként található. Ehhez integráljuk a 0 és a tartományba Rés ossza el vele R:
. (18)
Ugyanezt az eredményt kapjuk, ha a (13) kifejezést használva megtaláljuk a cső felületének elemi területére ható erőt, amely a cső középvonalára irányul, amelyre ez a kifejezés, figyelembe véve kifejezést (12) a 0 és a tartományba kell integrálni R:
(19)
Ezt az erőt elosztva az elemi terület méretével:
, (20)
megkapjuk a negatív nyomás értékét a cső belső felületén:
.
Ennek a nyomásnak köszönhetően a csőfalak közelében a statikus nyomás csökken. A keletkező statikus nyomást a következő kifejezés határozza meg:
(21)
Mivel a negatív nyomás nagysága a sebesség négyzetétől függ, teljesen természetes, hogy értéke az áramlás keskeny részén lényegesen nagyobb lesz, mint a szélesen. Ezért a Venturi-cső keskeny részén a nyomásmérők kisebb nyomást mutatnak, mint a széles részén. A csőfalakon fellépő negatív nyomás nagyságának függését a víz mozgási sebességétől a 9. ábra mutatja.
Egy másik példaként tekinthetjük a szórópisztoly működési elvét, amikor egy gázáram szívja be a folyadékot egy edényben (lásd 1. ábra). Úgy gondolják, hogy a folyadék beszívása annak köszönhető, hogy a gázáramban a sebessége miatt a nyomás a légköri nyomásnál alacsonyabb lesz, ami kipréseli a folyadékot az edényből, és a gázáram magával viszi. Ugyanezt a hatást fogja azonban okozni a negatív nyomás jelenléte, amelyet a permetezőfúvókából kilépő gázáram áramlásában a kinetikus energia nem egyenletes mezőjének jelenléte okoz. Ezenkívül a sugár magával viszi a környező levegő részecskéit, ami saját kinetikus energiamezőjének megjelenéséhez vezet, amelynek gradiense lesz az oka a folyadék felszívódásának az edényből.
Ekkor felmerül a kérdés: ha a Venturi-csőben és a szórópisztoly szívásában bekövetkező nyomáscsökkenés oka nem biztos, hogy a mozgó folyadék vagy gáz áramlásának nyomáscsökkenése, akkor hogyan érthetjük meg a Bernoulli-egyenlet lényegét? Hiszen a folyadék sebessége az áramlás beszűkült részében valójában növekszik, és ez, úgy tűnik, csak az ellenhatás csökkenésével lehetséges, és a kísérletek azt mutatják, hogy az áramlásban a nyomás alacsonyabb lehet a légkörinél, mivel a manometrikus csőben a folyadék a légköri nyomásnak megfelelő szint fölé emelkedik (10. ábra). Másrészt azonban az is tagadhatatlan, hogy az áramlás szűkítése növeli a mozgással szembeni ellenállást, és ezáltal növeli a nyomást a folyadékáramláson belül. Ebben az esetben az áramlási sebesség növekedése csak a hajtóerő növekedése miatt következhet be, pl. nyomást a kiemelt áramlási elem bal oldalán. Valójában hasonló következtetésre juthatunk, ha rátérünk a (7) egyenletre:

Nem szabad megfeledkeznünk arról, hogy ez az egyenlet az általunk izolált teljes folyadéktérfogatra vonatkozik, amelyet összességében tekintünk. Ezért nem lehet szétválasztani, ahogy az a (9) kifejezésben történik. Ezt nagyon fontos megjegyezni. A (7) kifejezésből az következik, hogy növekvő sebességgel V2állandó sebességgel V1 a nyomáskülönbség megnő p1És p2. Ez a növekedés akár csökkenés miatt is bekövetkezhet p2, és növekedése miatt p1. A Bernoulli-egyenlet elemzésekor szívesebben beszélnek nyomáscsökkenésről p2. De mi a nyomás p2? Ez az a nyomás, amely megakadályozza a folyadék vagy gáz mozgását. Hogyan határozzák meg? Vegyünk példának egy csővezeték kúpos fúvókáját (11. ábra). Egyértelmű, hogy az ellennyomás p2 A nyomás nem lehet kisebb a légköri nyomásnál, különben a folyadék nem fog kifolyni a fúvókán. Ha egy adott fúvókánál növelni akarjuk a folyadék áramlási sebességét, akkor a (7) egyenletnek megfelelően növelnünk kell a nyomást p1. De ez még nem minden. A sebesség óta V1És V2 egymásra épülő, növekvő sebességgel V2 a sebesség is növekedni fog V1, majd a nyomáskülönbség p1És p2 csökkennie kell, ami a nyomás növekedésének felel meg p2állandó nyomáson p1.
Így a Bernoulli-egyenlet elemzése problémát tár fel a lényegének megértésében. A probléma jobb megértése érdekében alkalmazzuk a (7) egyenletet a folyadék mozgásának tanulmányozására egy kúpos fúvókában (lásd 11. ábra). Az áramlás folytonossági feltételéből az következik, hogy az 1. és 2. szakaszban a sebességek a következő összefüggéssel függnek össze:
, (22)
Ahol R1És R2- keresztmetszeti sugarak az 1. és 2. szakaszban.
Ennek a sebességértéknek a behelyettesítése a (7) kifejezésbe és a sebesség megoldása V2, kapunk:
(23)
Elemezzük ezt a kifejezést. Vegyük a korlátozó összefüggéseket R2/R1. Nál nél R2/R1=0 sebesség V2 egyenlő lesz:
, (24)
mivel teljesen egyértelmű, hogy nullával kell egyenlőnek lennie. Igaz, a józan ész diktálja ezt a nyomást p1És p2 Pascal törvényének megfelelően egyenlőnek kell lenniük, különbségük pedig nullával egyenlő. Ez a körülmény azonban nem következik a (24) kifejezésből.
Nál nél R2/R1=1 sebesség V2 egyenlő lesz a végtelennel:
, (25)
ami persze nem lehet igaz. Azonban itt is találhat kiutat, ha kijelenti, hogy a nyomás p1És p2 is egyenlő lesz, mivel a sebességnek állandónak kell lennie. A sebesség nagyságát azonban nem fogjuk tudni megállapítani V2, mivel azt a nullák aránya fogja meghatározni.
De mi a helyzet az arány köztes értékeivel? R2/R1? A nyomáskülönbség nem lehet p1És p2 mindig nullával egyenlő legyen. Hogyan fog változni ez a különbség? Ezekre a kérdésekre nincs válasz. Csak egy dolog válik világossá: a Bernoulli-egyenlet még egy ideális folyadék esetében sem pontos, és nem használható sebességek vagy nyomások kiszámítására, valami hiányzik belőle. Ez az a kérdés, amellyel foglalkozni kell, és a digitális számításokkal.
Ilyen számítások, bár hozzávetőlegesek, léteznek a folyadék tartályból való kiáramlására vonatkozóan (12. ábra). A Bernoulli-egyenlet ebben az esetben, figyelembe véve a folyadék tömegéből származó potenciális energiát, a következőképpen alakul:
(26)
ahol g=9,81 m/s2 a nehézségi gyorsulás és a z koordináták 1 és z 2 valamilyen tetszőleges szintről számítanak, mivel a probléma megoldásához csak a különbségükre van szükség: H=z 1 - z 2 . Ez elfogadott V1=0, mivel V1<<V2, akkor a (26) kifejezésből kiderül:
, (27)
Ahol p2 megegyezik a légköri nyomással.
Ha p1 egyenlő lesz p2, akkor a (27) képlet még egyszerűbb formát ölt:
, (28)
amiből az következik, hogy a folyadék kiáramlási sebessége megegyezik a szilárd test szabadesésének sebességével H magasságból.
Ezt a kifejezést Toricelli 100 évvel Bernoulli előtt kapta, ezért nevezik Toricelli képletnek.
Az egyenlet levezetésének kézenfekvése ellenére azonban itt is felmerülnek kérdések, amelyekre nincs válasz: függ-e például a folyadék áramlási sebessége a furat méretétől, vagy a levehető kúpos fúvóka méretétől. a tartályhoz rögzítve (lásd 12,b ábra)? Hasonló lehet a folyadék áramlása egy kis lyukon keresztül a szabadeséshez? Ez persze még a sebesség hozzávetőleges meghatározásánál is nagyon kétséges.
A probléma elemzésének egyszerűsítésére vegyünk egy függőlegesen elhelyezkedő kúpos tartályt (13. ábra), amelybe folyadék áramlik és kifolyik, és így a szintje mindvégig változatlan marad. Figyelembe véve a (22) összefüggést a Bernoulli-egyenletből kapjuk:
(29)
Ebből a kifejezésből az következik, hogy mikor R2/R1=0 sebesség V2 csak akkor lesz egyenlő nullával, ha:
, (30)
amiből a következő:
, (31)
ami egyáltalán nem következik a probléma feltételeiből.
Nál nél R2/R1=1 V2=¥ , bár teljesen nyilvánvaló, hogy a folyadék leesik, ha a külső nyomás ellensúlyozza, ami megegyezik a légköri nyomással: p2=p0, és az esés mértékének nagyon konkrét értékkel kell rendelkeznie.
Így megállapítottuk, hogy a nyomás p2 folyadékáramlásban az aránytól függően változnia kell R2/R1 belül:
, (32)
amelynek változásának törvényét nem ismerjük.
Ennek az összefüggésnek a megállapításához vegyünk először egy zárt kúpos edényt, amelyben a gáz valamilyen nyomás alatt van (14. ábra). Ebben az esetben a gáz súlya, kicsisége miatt, figyelmen kívül hagyható. Pascal törvényének megfelelően a gáznyomás az edény minden pontján azonos lesz. Feltételezzük, hogy a nyomást az edényben az első szakasz oldaláról hozza létre az erő F1, amelynek értéke egyenlő lesz:
, (33)
Ahol S1- keresztmetszeti terület az első szakaszban. A második szakaszban a gáz erővel hat az aljára F2, egyenlő:
, (34)
Ahol p2=p1, S2- alsó terület.
Mivel a terület S2 kisebb terület S1, Kényszerítés F2 kevesebb lesz az erő F1. Teljesen nyilvánvaló, hogy a különbség ezek között az erők között:
(35)
az edény oldalfalainak ellenállása kompenzálja.
Így az edény szűkítése további ellenállást biztosít az erővel szemben F1, aminek következtében kisebb erő hat majd az aljára.
Most távolítsuk el az edény alját. Mivel az edényben lévő gáz nyomása nagyobb, mint a légköri nyomás, bizonyos sebességgel elkezd kifolyni az edényből. Ez a mozgás csak a gáznyomás csökkenése miatt következhet be, mivel a gáz mozgásának kinetikai energiája csak a nyomásának potenciális energiája miatt jelenhet meg. Nyilvánvaló, hogy ebben az esetben az első és a második szakaszban a nyomás közötti kapcsolatnak meg kell változnia, mivel a bennük lévő gázrészecskék mozgási sebessége eltérő lesz, és ezért a potenciális energia (nyomás) mozgási energiává alakul át. is más lesz.
Most már csak azt kell kitalálni, hogyan fog változni a nyomás mindkét szakaszban, ha a gázsebesség bennük V1És V2és a statikus nyomás p1állandó szinten marad. Mivel a mozgás forrása csak a gáznyomás, a potenciális energia csökkenése miatt, aminek a mozgási energiája megjelenik, teljesen ésszerű az energiamegmaradás törvényét alkalmazni, feltételezve, hogy nincs energiaveszteség. Egyébként az egyenlet levezetésénél Bernoulli is ezt a törvényt használta, mivel a nyomóerők minden munkája mozgási energiává alakult.
Az energiamegmaradás törvényének megfelelően az első és a második szakaszban a statikus nyomások kisebbek lesznek a kezdetieknél a bennük lévő térfogati kinetikus energiasűrűség mértékével:
; (36)
, (37)
mert p2=p1.
Ezekből az összefüggésekből kitűnik, hogy mindkét szakaszban kapcsolatot hozunk létre a nyomások és a sebességek között, és a második szakasz nyomása az első szakasz nyomásától függ. Sebesség V1És V2 egymástól is függenek. Tehát vitatható, hogy a nyomások kölcsönösen függenek egymástól.
Ha a nyomásokhoz hozzáadjuk a mozgási energiává alakított potenciális energia veszteségeket és , akkor az első és a második szakaszban a statikus nyomás egyenlő lesz és egyenlő lesz. p1, azaz:
, (38)
amely a Bernoulli-egyenlet analógja.
Így megkaptuk a Bernoulli-egyenletet, amely az energiamegmaradás törvényén alapul egy ideális folyadék egyenletes áramlásához. Lényegében a Pascal-törvény hatályát kiterjesztettük egy mozgó folyadékra.
Az első és második szakasz nyomásváltozása miatt a bennük ható erők is megváltoznak. A (36) és (37) kifejezésekkel összhangban ezeknek az erőknek a nagysága egyenlő lesz:
; (39)
(40)
Lássuk, mi történik az ellenerővel D.F. Ha ezt az erők és a különbségeként határozzuk meg, azt kapjuk:
, (41)
amiből az következik, hogy a falak felől érkező ellenerő növekszik.
A vizsgált példából és az általunk megfogalmazott feltételezésekből a következő következtetések vonhatók le.
Először is, annak a csatornának a szűkülése, amelyen keresztül egy folyadék vagy gáz mozog, ellenállást mutat ezzel a mozgással szemben, amelynek nagysága a szűkület mértékétől függ, pl. minél nagyobb a szűkítés, annál nagyobb az ellenállás. És ennek az ellenállásnak a jelenléte nem függ attól, hogy a folyadék melyik csatornán áramlik át - széles csövön vagy elemi áramban. Az ellenállás mértéke az áramlási sebességek arányától is függ a különböző szakaszokban, amint az a (41) képletből következik. A Bernoulli-egyenlet levezetésekor ezt az ellenállást nem vesszük figyelembe.
Másodszor, a második szakasz nyomása az első szakasz nyomásától függ, egyenlő:

A nyomás a második szakaszban a folyadék áramlási sebességétől is függ, egy mennyiséggel csökken. Ebből az következik, hogy a nyomás nem külső ellenállás a folyadék egy kiválasztott eleméhez képest, hanem az adott folyadékrész belső tulajdonsága. Ez pedig lényegében az a nyomás, amit a folyadék felszabaduló eleme a folyadék későbbi, kidobott részére gyakorol, pl. olyan erőt hoz létre, amely a következő folyadékrészek mozgását idézi elő. És ami nagyon fontos, ez a nyomás nem fog közvetlenül függni a kiválasztott folyadékelemen kívüli nyomástól a kidobott, következő folyadékrész oldaláról, amit -vel jelölünk. Itt a függés közvetett lesz: a sebesség a nyomástól függ V1És V2, és már a sebességtől V2 nyomás attól függ. Megjegyzendő, hogy a nyomás egyik összetevője általában a környezeti nyomás, különösen a légköri nyomás. Ez közvetlenül következik abból, hogy a folyadékáramban a nyomás nem lehet kisebb a légköri nyomásnál. A fentiekből tehát az következik, hogy a Bernoulli-egyenlet levezetésénél a nyomást nem szabad figyelembe venni az ellenállási erő megjelenésének okaként - az ellenállási erőt csak a nyomás hozza létre.
Harmadszor, a D húzóerő F, amely a csatorna szűkülése miatt keletkezik, csak az első és a második szakasz erőkülönbsége határozza meg, és közvetlenül ellensúlyozza az erőt, pl. feltételezhetjük, hogy az első részben alkalmazzuk. Mert az erőt a nyomás határozza meg, a nyomástól függő p1, majd az ellentétes erő D F nyomástól is függ p1és ezért mintegy önfékező ereje a folyadékáramlásnak, amikor az a szűkített részben mozog. Ezért a Bernoulli-egyenlet levezetésekor a D erő F, egyrészt figyelembe kell venni, másrészt a munkájának meghatározásához meg kell szorozni a folyadék bal végének mozgásával D l1.
Összegzésként elmondható, hogy az általunk levont összes következtetés azért vált lehetségessé, mert a kiválasztott folyadékelem mozgását egyetlen egész testnek tekintettük, nem pedig két, a végein elhelyezkedő kis szakasznak. Nyilvánvaló, hogy ez a megközelítés felel meg a legpontosabban a feladatnak.
Most térjünk vissza a kúpos tartályból való víz kiáramlásának problémájához (lásd 13. ábra). Folyadékos tartályban a második szakaszban nyomás van, amely a reakcióerőt határozza meg DF kivéve a nyomást p1 nyomás is meghatározza rn a folyadék súlya által létrehozott:
, (42)
Ahol N- a folyadékoszlop magassága a felső szintjétől mérve, amellyel kapcsolatban a (36) és (37) kifejezések a következő alakot öltik:
; (43)
(44)
A fentiekkel összefüggésben meg lehet határozni a kiválasztott folyadékelemre ható erőket:
; (45)
; (46)
(47)
Ezenkívül figyelembe kell venni a folyadék következő részéből származó ellenállási erőt:
, (48)
ahol ebben az esetben egyenlő lesz a légköri nyomással ro.
A vizsgált folyadék térfogatára vonatkozó mozgásegyenlet összeállításánál csak az és erőket kell figyelembe venni, mivel fentebb bemutattuk, hogy az erő nem ellenállási erő. Azt is kimutatták, hogy amikor megtalálták az erők munkáját és D F ezeket meg kell szorozni a folyadék mozgásával az első szakaszban - D l1. Tisztázni kell azt a kérdést, hogy hogyan kell kezelni az ellenállási erőt: milyen D elmozdulás l meg kell szorozni D-vel l1 vagy D l2? A probléma megoldásához kombináljuk a D erőket FÉs:
(49)
amelyből azt kapjuk, hogy a zárójelben lévő második kifejezés a folyadék túlnyomását jelenti a második szakaszban lévő nyomáshoz viszonyítva:
(50)
Ebből következik, hogy egy erő munkáját úgy kell meghatározni, hogy megszorozzuk az elmozdulással Dl1.
Így ennek a problémának a mozgásegyenletét a mozgási energia változásának törvénye formájában a következő kifejezés határozza meg:
(51)
A (45) és (49) kifejezések által meghatározott erők megfelelő értékeinek behelyettesítése után az (51) kifejezés a következő alakra alakul:
(52)
amely a termékkel való felosztás után S1 D l1és a megfelelő átalakítások a következő formában lesznek:
(53)
Sebesség kifejezése V1 sebességen keresztül V2 a (22) kifejezésnek és a sebességre vonatkozó (53) egyenlet megoldásának megfelelően V2, megkapjuk a számítási képletet:
(54)
Elemezzük ezt a képletet. Nál nél R2/R1=0 sebesség V2 egyenlő lesz nullával, mivel a számláló nulla, a nevező pedig egy lesz. Nál nél R2/R1=1 sebesség V2 egyenlő lesz:
, (55)
ami egybeesik a (27) kifejezéssel. És ez a kifejezés ebben az esetben valóban megfelel a folyadék szabadesésének, hiszen R2=R1. Az arány köztes értékeinél R2/R1 sebesség V2 ennek a kapcsolatnak megfelelő jelentése lesz. Ennek a sebességnek a kiszámításának eredménye === n/m2 és at N=10,2 m a 15. ábrán látható. Ahogy az várható is, az arány növekedésével R2/R1 a sebesség simán növekszik nulláról a szabadesésnek megfelelő maximális értékre. Ezenkívül a (44) képlet segítségével meghatározható a nyomás egy kúpos tartályból folyó folyadékáramban. Ennek a képletnek az elemzése azt mutatja, hogy mikor V2=0 a folyadék nyomása egyenlő lesz:

és at , ami a szabadesésnek felel meg, =. A nyomás =+= számított görbéje a 15. ábrán látható, amelyből látható, hogy a kiáramló sugárban a nyomás minden sugárarány esetén nagyobb lesz, mint a légköri nyomás R2/R1, kivéve, ha ezek a nyomások egyenlőek.
Hogy minden elmondott meggyőzőbb legyen, adjuk meg a mozgásegyenlet egy másik levezetését, figyelembe véve az ideális folyadék kiválasztott elemére ható tehetetlenségi erőket. Ebben az esetben a mechanika törvényei alapján a kérdéses folyadékelemre ható erők egyensúlyban lesznek.
A tehetetlenségi erő meghatározásához vegyük figyelembe a kúpos csatorna azon részét, amelyen keresztül a folyadék mozog (16. ábra). Válasszuk ki a folyadék elemi térfogatát dm, amely az első pozícióból a másodikba mozog, és tömegközéppontjának sebességét értékről értékre változtatja. A kapott elemi tehetetlenségi erő a következő képlettel határozható meg:
, (56)
Ahol
, (57)
a mínusz jel pedig a tehetetlenségi erő irányát mutatja.
A sebességek kapcsolata az elemi tömeg két figyelembe vett helyzetében dm kifejezés határozza meg:
, (58)
Ahol
(59)
Ezt az összefüggést használva a következőket kapjuk:
(60)
Emeljük a binomiálist a negyedik hatványra, és minden tagot elosztunk D-vel ls majd elfogadta D ls nullával egyenlő kifejezést találunk az elemi tehetetlenségi erőre:
(61)
Tegyük fel, hogy a lényeg Si távol van l az első szakasztól kezdve a szakaszok sebességének és sugarának aránya ezekben a pontokban a következő lesz:
; (62)

(63)
Ha ezeket a sebesség és sugár értékeket behelyettesítjük a (61) kifejezésbe, a következőt kapjuk:
(64)
Most összegezni kell az elemi tehetetlenségi erőket a mozgó folyadék teljes kiválasztott térfogatára, azaz. hossz szerint l. A tömegérték behelyettesítése kifejezésbe (64) dm:
(65)
és a (64) kifejezés integrálját a 0 és a tartományba vesszük L, keressük meg a teljes mozgó folyadék tömegére ható tehetetlenségi erőt az első szakaszon, ahol a hajtóerő érvényesül F1:
(66)
Ahol .
A (66) kifejezésből az következik, hogy a tehetetlenségi erő ténylegesen az első szakaszra vonatkozik, mivel a második és az első szakasz energiasűrűségének különbsége (a zárójelben lévő kifejezés) megszorozzuk az első szakasz területével.
Így a következő erők hatnak a felszabaduló folyadék térfogatára:
;
;
;
, (67)
melynek hatására ez az általunk egyetlen testnek tekintett folyadéktérfogat a mechanika törvényeinek megfelelően egyensúlyba kerül, azaz. a következő feltétel teljesül:
, (68)
amely az összes erő értékének helyettesítése után a következő formára alakul:
(69)
A kifejezések csökkentése és osztás után S1 A (69) kifejezés a következő formában jelenik meg:
,
amely teljesen egybeesik a korábban kapott kifejezéssel (53). Ezért az érvelésünk igazságos volt, és az ebből eredő képletek a sebesség meghatározására V2és a nyomások megfelelőek.
Így úgy tűnik, hogy megoldottuk a folyadékáramlás sebességének meghatározását. Ha azonban a helyzetet a mechanika törvényei felől fogjuk fel, kétségek merülnek fel a kapott képletek érvényességével kapcsolatban. Valóban, ha példaként egy állandó keresztmetszetű csőből kifolyó, függőlegesen leeső folyadékáramot nézünk (17. ábra), akkor azonnal észrevehetjük, hogy a folyadék áramlása még a csövön kívül is mozog. egyetlen testként a csőben lévő folyadékkal, és ezért minden pontjában azonos sebességűnek kell lennie. Ha ez nem történik meg, az áramlás megszakad, mivel a gravitáció hatására a sebességnek folyamatosan növekednie kell. A gyakorlatban azonban ilyen hiányosság nem figyelhető meg. Ez a körülmény a folyékony molekulák közötti adhéziós erők (kohézió) jelenlétéből adódik, és ezek az erők meglehetősen nagyok lehetnek. Tehát tiszta, szennyeződésmentes víznél a szakítószilárdsága eléri a 3107 N/m2-t, ami 300 atm-nek vagy 3000 m-es vízoszlopnak felel meg. Teljesen nyilvánvaló, hogy a kohéziós erőknek egy ideális folyadékban kell létezniük. Ezért amikor bármely folyadékelem elmozdul r m rajta, kivéve a gravitációt Fstrand az ellenállási erő is hatni fog Fresistance a folyadék felső részeitől és a hajtóerőtől Fdv az alsó oldalról. Az r folyadékelem szabadesése következtében m nem fog, és maga az elem a rá ható erők hatására húzó alakváltozásokat szenved, amelyek hatására keresztirányban összenyomódik, és a teljes áramlás összességében szűkül (a 17. ábrán a szűkület az áramlást szaggatott vonalak jelzik). Ennek a szűkületnek köszönhetően az elem sebessége dm ahogy esik, változnia kell, és a sebesség sem V1, sem sebesség V2 nem ismertek számunkra, és amint az érvelésünkből következik, a fenti képletekkel nem találhatók meg.
Annak érdekében, hogy valahogy kikerüljünk ebből a helyzetből, legalább megközelítőleg vegyük figyelembe, hogy az áramlás csövön kívül kiáramló része milyen hatással van a csőben elhelyezkedő folyadékra. Ez a külső hatás húzó lesz, i.e. ez további nyomást fog okozni rd az áramlásban, megkönnyítve annak mozgását. A külső húzóerő nagyságát a csövön kívül elhelyezkedő folyadékoszlop súlya határozza meg. Mivel az áramlás csökkenésével csökken, a folyadékoszlop tömege megegyezik a vízkúp tömegével (18. ábra):
, (70)
Ahol mh- a folyadékoszlop tömege, R2És Rh- az oszlop sugarai az áramlás figyelembe vett részének elején és végén. Pólus magasság h, nyilván függ az áramlási esés adott magasságától, például valamilyen edénybe, vagy a folyadék részecskéi közötti tapadás elvesztésétől, amikor elvékonyodik, amikor az áramlás egyes cseppekre bomlani kezd. Meg fogjuk adni az értéket hönkényesen, anélkül, hogy figyelembe vennénk a sugár tönkremenetele szempontjából kritikus helyzeteket, mivel ez a kérdés speciális kutatást igényel.
Egy ismert sugarú folyadékoszlop tömegének meghatározásához szükséges R2 keresse meg a sugarat Rh, az esési magasságnak megfelelő h. Ennek a sugárnak a hozzávetőleges meghatározásához vegyük figyelembe valamilyen tömegű folyékony elem esését Dm a magasból h csak saját súlyának hatására, bár mind a felső, mind az alsó oldalról tapadási erők érik, amelyek aránya a kiválasztott elem leesésével változik.
Newton második törvényének megfelelően a következők lesznek:
(71)
Ezt az egyenletet a kezdeti feltételekkel oldjuk meg:
(72)
Ennek eredményeként a következőket kapjuk:
; (73)
(74)
A (74) kifejezésből megtaláljuk az esési időt t:
(75)
Ennek az értéknek a helyettesítése t a (73) kifejezésbe, megkapjuk az esés sebességének függőségét Vh koordinátából h:
(76)
Az áramlás folytonossági feltételének használata:
, (77)
kapunk:
(78)
ábrán. A 19. ábra az arányszámítások eredményeként kapott folyadéksugarak alakjait mutatja be Rh/R2 a (78) képlet szerint a kipufogógáz sebességére V2 0,1 m/s és 0,5 m/s, az esés magasságától függően h. Az ábrákból jól látható, hogy kis kiáramlási sebességnél a sugár szűkülése élesebb lesz.
Ahhoz, hogy figyelembe vegyük a járulékos hajtóerő hatását az áramlás sebességére és a benne lévő nyomásra, figyelembe kell venni az általunk kapott egyenletekben. Ezt úgy tehetjük meg, hogy az első szakaszhoz rendeljük, ahol a nyomás által meghatározott hajtóerő hat p1és keresztmetszeti terület S1. Ekkor a további erő által létrehozott nyomás egyenlő lesz:
(79)
Kényelmesebb ezt a kifejezést a következő formában megjeleníteni:
, (80)
mert akkor a hozzáállás Gh/S2 egyszerű formája lesz:
, (81)
és a (80) kifejezés a következő alakra alakul:
(82)
Ezután a második szakaszban a sebességek és nyomások számítási képleteit, figyelembe véve az adhéziót, a korábban kapott képletek szerint határozzuk meg a következő kifejezéssel:
; (83)
(84)
Nál nél R2/R1=1 képlet (83) a következő formában lesz:
, (85)
és mikor ==:
, (86)
A 20. és 21. ábrán a sebességek és nyomások számítási eredményei láthatók anélkül, hogy figyelembe vették volna a folyadékon belüli tapadást annak a kúpos edénynek a magasságában, amelyből a folyadék 10,32875 m és 1 m magasságban folyik. Az első magasság a légköri magasságnak felel meg nyomás. Mindkét esetben a magasság h egyenlőnek vették NÉs N/R1=10, =.
Ahogy a görbékből is látszik, az áramlási sebesség az esési magasság miatt jelentősen megnőhet h. Ezzel a kiáramlási sebesség értéke közelebb kerül a Toricelli képlet által meghatározott eredményhez. A sugár belsejében a nyomás megnő, mivel az áramlási sebesség növekedése miatti vesztes nyomás (potenciális energia) egy részét a hozzáadott nyomás kompenzálja. Azonban a folyadék szabad esésével at R2/R1=1 nyomás mindkét esetben egyenlő lesz a légköri nyomással.
Így az általunk kapott képletekkel hozzávetőlegesen meg lehet határozni az áramlási sebességeket annak különböző szakaszaiban, és ezek a sebességek nagymértékben függenek a nagyságtól. h(lásd 22. ábra, a és b).

Érdekesnek tűnik egy cső kimeneténél a folyadékáram felfelé mozgásának problémája is (23. ábra). Ebben az esetben a 2-2 szakaszban további ellenállási erő hat az áramlásra, amely megegyezik a folyadékáram külső magasságú részének súlyával. h. Ez az erő további nyomást hoz létre a második szakaszban, amelynek értéke megközelítőleg egyenlő lesz:
(87)
(feltételezzük, hogy az áramló folyadékoszlop hengeres alakú).
Ez a nyomás a nyomás összetevőjeként szerepel, ami szerepel a számítási képletekben. Ezután a nyomást a következő kifejezés határozza meg:
(88)
Teljesen nyilvánvaló, hogy a sebesség V2 csökkenni fog. Számolni azonban V2 tudnia kell az emelési magasságot h, ami viszont a kipufogó sebességétől függ V2. Ezért h valahogyan a sebességben kellene kifejezni V2. A következőképpen érvelünk. Áramlási elem r m a 2. szakaszban van valamilyen mozgási energiája, ami az áramlás felső részében potenciállá alakul. Ezért a következő összefüggésnek teljesülnie kell:
, (89)
honnan kapjuk:
(90)
Ekkor a nyomás így fog kinézni:
(91)

Ezt a nyomásértéket be kell cserélni az eredeti (53) egyenletbe, amely a megoldást követően a V2 a következő kifejezést adja:

(92)
Állandó keresztmetszetű csőhöz, pl. nál nél R2/R1=1, ez a kifejezés a következő formában lesz:
, (93)
és mikor p1=p0 kapunk:
(94)
Ezt a sebességértéket a (90) kifejezésbe behelyettesítve azt kapjuk, hogy:
(95)
Így a folyadék emelkedésének magassága kétszer kisebb lesz, mint a szintkülönbség H. Ne feledje, hogy ezek a sebesség hozzávetőleges értékei V2és emelési magasságok h, mivel a külső áramlás keresztmetszete nem maradhat állandó: a sebesség csökkenése és az áramlás folytonosságának feltétele miatt a kimenettől való távolság növekedésével kell növekednie. Ezenkívül az áramlás keresztmetszetének értékét az áramlás lefelé irányuló része is befolyásolja, ami olyan húzóerőt hoz létre, amely növeli az áramlás sebességét.
Becsült sebességértékek V2, nyomás és magasság h vízemelkedést mutatunk be a 20. és 21. ábrán két olyan esetre, amikor N=10,32875 m és N=1 m. A nyomást ebben az esetben a szokásos képlet határozza meg:

Mivel az áramlási sebesség ebben az esetben kisebb lesz a vízoszlop járulékos ellenállása miatt, a nyomás nagyobb lesz, mint amikor a folyadék lefelé áramlik, ha nem vesszük figyelembe a tapadás miatti többleterő jelenlétét folyékony részecskékből.
Tekintsük most nem egy ideális, hanem egy valódi viszkózus folyadék mozgását. A folyékony rétegek fékezése a csőfalakon és egymás között a folyadékrészecskék mozgási sebességének csökkenéséhez, következésképpen az áramlás kinetikus energiájának egy részének elvesztéséhez vezet. Az áramlás kinetikus energiájának meghatározásához egy tetszőleges szakasz sugara mentén definiáljuk a sebességváltozás törvényét a következő formában:
, (96)
Ahol VlÉs Rl- a folyadék sebessége az áramlási tengelyen és a keresztmetszeti sugár távolságban l az első szakasztól. A kinetikus energiát az átlagos áramlási sebességből kell meghatározni, amely a folyadék térfogatáramából állapítható meg K:
, (97)
Ahol Sl- keresztmetszeti terület távolságban l. A (97) kifejezésből a következőket kapjuk:
(98)
A térfogati áramlási sebességet a (96) kifejezés segítségével találjuk meg elemi gyűrű alakú szakaszokra, amelyek területét a következő kifejezés határozza meg:
, (99)
Ahol dr- gyűrű szélessége. Ennek megfelelően az elemi térfogatáram egyenlő lesz:
(100)
Ennek a kifejezésnek a 0-tól való integrálásával R, megkapjuk a szakaszban lévő folyadék teljes térfogatáramát l:
(101)
A (98) képlet segítségével megtaláljuk az átlagos áramlási sebességet a keresztmetszetben l:
(102)
Az áramlás kinetikus energiája egy bizonyos D területen l ebben az esetben egyenlő lesz:
, (103)
ahol D m-D hosszának megfelelő l a folyékony terület tömege.
Egy kiválasztott folyadéktérfogat mozgásegyenlete erőösszeg formájában, figyelembe véve a súrlódási erőt Ftr a következő kifejezés határozza meg:
(104)
Ez a kifejezés figyelembe veszi a keresztmetszeti átlagos áramlási sebességeket az 1. és 2. szakaszban. A súrlódási erőt a meglévő kísérleti adatokból kell meghatározni.
A szükséges átalakítások elvégzése után a (104) kifejezést a következő alakra redukáljuk:
(105)
hol találjuk a sebességet? V2:
, (106)
Ahol
(107)
nyomásveszteség a hossz mentén L=H(ennyivel csökken a nyomás p1 a 2. szakaszban).
Ennek a kifejezésnek az elemzése azt mutatja, hogy mikor R2/R1=0 sebesség V2 egyenlő lesz nullával, és mikor R2/R1=1 kifejezés (107) a következő formában lesz:
(108)
Az átlagos áramlási sebesség a második szakaszban kétszer kisebb lesz.
A második szakaszban a nyomásérték csökkenni fog a súrlódási erők leküzdéséhez szükséges energiaveszteség miatt, és a következő kifejezés határozza meg:
(109)
Amikor egy folyadék lefelé mozog, figyelembe kell venni az intermolekuláris kohéziót. Aztán a sebesség V2 a következő kifejezés határozza meg:
(110)
Amikor a folyadék függőlegesen felfelé áramlik, a nyomás, amint az fent látható, a következő kifejezéssel ábrázolható:
(111)
Aztán a sebesség kifejezése V2 a következő formában lesz:
(112)
A folyadék belsejében lefelé és felfelé mozgó nyomást a (109) kifejezés határozza meg, csak a sebesség V2 természetesen mások lesznek. Ez azt jelenti, hogy a nyomások eltérőek lesznek.
A folyadékon belüli nyomás, figyelembe véve annak összenyomódását, a (18) képlet szerint az átlagos negatív nyomás mértékével nagyobb lesz:
,
a falközeli nyomás ennyivel kisebb, azaz:
; 113)
(114)
A folyadékáramlás sebességének és a benne lévő nyomás kiszámításához, figyelembe véve a súrlódási erőt, meg kell határozni a súrlódási erőt. Ehhez a Poiseuille-képletet használjuk, amely lamináris áramlási rendszerben határozza meg a folyadék áramlási sebességét:
, (115)
Ahol K- folyadék áramlási sebessége m3/s-ban, p1-p2- nyomásesés a folyadékáramban egy hengeres cső hosszúságú szakaszán L N/m2-ben, m- a folyadék dinamikus viszkozitása kg/ms-ban, d- csőátmérő m-ben.
Ezzel a kifejezéssel megtalálhatja az átlagos sebességet a cső keresztmetszetében:
, (116)
ahol, mint fentebb megjegyeztük, az átlagos sebesség egyenlő a maximális tengelyirányú sebesség felével V.
A (116) kifejezés segítségével megtaláljuk a hossz menti súrlódás miatti nyomásveszteséget L:
(117)
Mivel változó keresztmetszetű edényt (csövet) vizsgálunk, a (117) kifejezést differenciális formában írjuk:
, (118)
Ahol Vl- axiális sebesség az első szakasztól távol eső szakaszon l, Rl- ennek a szakasznak a sugara, dl- az elemi nyomásveszteségnek megfelelő szakasz elemi hossza dp(24. ábra).
A további átalakításokhoz az áramlás folytonossági feltételét használjuk:
,
hol találjuk:
, (119)
Ahol
(120)
Ezeket a kifejezéseket használva a következőket kapjuk:
(121)
Az eredményül kapott kifejezés átintegrálásával l 0-tól L, keressük meg a nyomásveszteséget a teljes hosszon L:
(122)
Mivel a zárójelben lévő kifejezés:
, (123)
egy tg a kifejezés határozza meg:
, 124)
a (122) képletet a következő alakra alakítjuk:
(125)
Fogalmazzuk meg a sebességet V1 sebességen keresztül V2, az áramlás folytonossági feltételével:
(126)
és redukáljuk a (125) kifejezést a következő alakra:
(127)
A kapott képletek felhasználásával három számítási lehetőséget készítettek a következő méretű kúpos csövekre:
1) H=L=10,32875 m (ami a légköri nyomásnak felel meg);
2) H=L=1,0 m;
3) H=L=0,1 m
Minden esetben az arány H/R1 10-nek vették, h=H, a vizet folyadéknak vettük, amelyre a dinamikus viszkozitási együttható m egyenlő 0,001 kg/ms. A számítások azt mutatták, hogy a kiválasztott csőméreteknél az átlagos vízáramlási sebesség viszkozitás jelenlétében gyakorlatilag nem különbözik az ideális folyadék sebességétől, amit a 15. ábra grafikonja mutat be. Ez az együttható kis értékének köszönhető. m. A sugárban lévő nyomás, anélkül, hogy figyelembe vennénk a molekulák közötti adhéziót és annak összenyomódását, a kinetikus energiamező gradiensének jelenléte miatt, szintén megegyezik az ideális folyadékéval. Ha ezeket a tényezőket figyelembe vesszük, akkor a sugár belsejében lévő nyomás jelentősen megnőhet, és a falközeli nyomás csökkenhet, ami a légkörinél kisebb lesz, sőt negatív is lehet. Három lehetőség számítási eredményeit a 25-27. Az ábrákon a nyomás és a nyomás változását jellemző görbék láthatók
relációs függvények R2/R1, amikor az áramlás lefelé mozog a tengelykapcsoló figyelembevétele nélkül
folyadékmolekulák közötti kölcsönhatások (1. görbe), amikor az áramlás lefelé mozog a molekuláris kohézió figyelembevételével (2. görbe) és amikor az áramlás felfelé (3. görbe). A görbékből látható, hogy a nyomásváltozások a nagyobb csőméreteknél a legjelentősebbek, ezért könnyen megfigyelhetők.
Megvizsgáltuk tehát, hogyan változik a benne lévő áramlási sebesség és nyomás, amikor egy változó keresztmetszetű csövön átfolyik egy folyadék. A számítások azt mutatják, hogy a viszkózus folyadék nyomása a cső kimeneténél nagyobb lesz, mint a légköri nyomás. Nyilvánvaló, hogy ez a nyomás egy ideig nagyobb lesz, mint a légköri nyomás, még akkor is, ha a folyadék a csövön kívülre kerül. Nézzük meg közelebbről ezt a kérdést.
Ha a folyadék nyomása a lyukból való kilépésnél nagyobb, mint a légköri nyomás, akkor a sugárnak azonnal ki kell tágulnia a kilépésnél, de ez nem történik meg, a sugár még össze is húzódik. Ennek okát már tárgyaltuk. Először is, ez a kinetikus energiamező gradiensének megmaradásával magyarázható, ami az áramlás középpontjában és a szélei mentén tapasztalható sebességkülönbségnek köszönhető, amelyek még nem egyenletesek. A gradiens által meghatározott erő továbbra is összenyomja az áramlást. Másodszor, a folyadékáramot a folyadékáram által magával vitt levegő mozgása által generált erő összenyomja. Ebben az esetben a légáramban egy kinetikus energiamező is megjelenik, melynek gradiense határozza meg a ható erőt.
Határozzuk meg azt a nyomást, amellyel a levegő összenyomja a folyadékáramot. A 28. ábra a levegő sebességi mezőjének mintázatát mutatja, amely a következő kifejezéssel jellemezhető:
, (128)
Ahol r- távolság a sugár középpontjától.
Ekkor valamilyen elemi tömeg mozgási energiája dm egyenlő lesz:
, (129)
Ahol
(130)
Itt: rв- levegő sűrűsége.
Ennek a kifejezésnek a deriváltja határozza meg az elemi erőt dFв:
,(131)
az áramlás közepe felé irányítva.
Ennek az erőnek az elemi felülethez viszonyított aránya dS=rdjdh, amely az elemi tömegnek felel meg, meghatározza a nyomáskülönbséget dpv:
(132)
(a mínusz jelet elhagyjuk).
A külső levegőrészecskék elemi tömegére ható össznyomást a (132) kifejezés integrálja határozza meg, amelyet r-től az r-ig terjedő tartományban vesz át:
(133)
A sugár felszínén ( r=Rh) a légnyomás egyenlő lesz:
(134)
Harmadszor, a sugár összenyomódik a folyadékmolekulák közötti tapadás által okozott húzóerők jelenléte miatt, valamint, amint azt fentebb megjegyeztük, a gravitáció hatására megnövekedett esési sebesség miatt.
Negyedszer, a sugár összenyomódik a felületi feszültség jelenléte miatt.
Így a csőből kiáramló folyadékáramra több erő hat majd, ezek kombinációja határozza meg mind az alakját, mind a benne lévő nyomást, és amelynek befolyását matematikailag nehéz figyelembe venni.
Próbáljuk meg azonban ezt legalább megközelítőleg megtenni. Mivel a sugár jól körülhatárolható kúpos alakú, feltételezhetjük, hogy a folyadék mozgása a sugárban hasonló lesz, mint egy elkeskenyedő csatornában (csőben), és ismerjük a sebességeket a sugár elején és végén. mozgalom V2És Vh, valamint a nyomás a sugár csőből való kilépésénél. Sebesség Vh a gravitáció hatására bekövetkező mozgás által okozott mozgás, amint fentebb bemutattuk, a hozzávetőleges kifejezés határozza meg:

A probléma megoldásához feltételezzük, hogy a sebességnövekedés csak a sugár potenciális energiájának felhasználása miatt következik be, pl. belső nyomásának csökkentésével. Egy ilyen feltételezés bizonyos mértékig lehetséges, ha emlékezünk arra, hogy a folyadék gravitációs hatása alatti mozgását a részecskéi (molekulái) közötti tapadás okozta erők akadályozzák meg, pl. összetartó erők.
Mivel az áramlási mozgást semmilyen csatorna nem alakítja ki, és a sugár tömege nem vesz részt a többletnyomás létrehozásában, ezért a Bernoulli-egyenletet tiszta formájában használjuk:
, (135)
hol találja a nyomást ph:
(136)
A sebesség kifejezés használata Vh, a (136) egyenletet a következő alakra alakítjuk:
(137)
Az eredményül kapott kifejezés felhasználható az áramlásesés magasságának meghatározására h, amelynél a nyomás ph egyenlő lesz a légkörivel:
(138)
Az általunk vizsgált három példa esetében mikor H»10 m, H=1m és H=0,1m az értékek rendre megegyeznek:
1) m
2) m
3) m
Mindhárom esetben a sugár esésének magassága, amelynél a belső nyomás megegyezik a légköri nyomással, körülbelül 4-szer nagyobb, mint a magasság h=H. Természetesen ezek, mint már említettük, hozzávetőleges értékek, amelyeket kísérletileg kell ellenőrizni.
Az általunk vizsgált összes példa meggyőzően mutatja, hogy az ideális és a valódi folyadék sugárában a nyomás nem lehet alacsonyabb a légköri nyomásnál. A falnyomás azonban lényegesen kisebb lehet, ami nyomócsövek használatakor nyilvánul meg. A (114) kifejezés segítségével a manometrikus cső segítségével talált nyomást használhatja a folyadékáramlás nyomásának meghatározására:
(139)
A második kifejezés ebben a kifejezésben valójában egy módszertani mérési hiba, mivel ez nem eszközhiba vagy véletlenszerű hiba, hanem magával a mérési módszerrel kapcsolatos hiba.
A (114) képlet segítségével meghatározható a folyadék mozgásának sebessége egy csővezetékben, kísérletileg megállapított ismert falnyomás mellett. Ehhez bővített formában kell bemutatni, figyelembe véve a (109) és (107) kifejezéseket:
(140)
Tekintsünk két nyomásmérési esetet, amelyeket a 7. és 10. ábra mutat be. Az első esetben (7. ábra) az 1. és 2. szakaszban látható manometrikus csövek által mutatott nyomások h értékkel térnek el az ezekben a szakaszokban tapasztalható folyadéksebesség-különbség miatt. . A vízszintes cső falnyomása a (140) képlet szerint egyenlő lesz:
; (141)
, (142)
ezért különbségüket a következő kifejezés határozza meg:
(143)
A (22) reláció segítségével a (143) kifejezésből megtaláljuk a sebességet V1:
(144)
A második esetre (10. ábra) a fal és a légköri nyomás között egy szűk szakaszon összefüggést állapítunk meg kapcsolat formájában:
, (145)
Ahol rm- a folyadék sűrűsége a manometrikus csőben, h- a csőben lévő folyadék magassága az edényben lévő folyadékszint felett légköri nyomáson. A (145) kifejezésből megtaláljuk a folyadék áramlási sebességét V:
(146)
Most keressük meg a hibát a folyadékáramláson belüli nyomás szondával történő mérésénél (29. ábra). Tekintsük azt az esetet, amikor a szondacső az áramlási tengely mentén helyezkedik el. A cső jelenléte az áramlási mozgás jellegének megváltozásához, a benne lévő sebességmező mintázatának megváltozásához vezet (30. ábra), mivel a cső a cső falaihoz hasonlóan lelassul. a folyadék áramlása. A sebességmező az áramlási sebesség maximális értékét tekintve két részre osztható Vm: első rész - a sugárszonda csőből r3 sugárig rm, amely a maximális sebességnek felel meg, és a második rész - tól rm a csőfalhoz, azaz. sugárig R.
Tegyük fel, hogy ezekben a szakaszokban a sebességmezőt a következő kifejezések határozzák meg:
; (147)
(148)
Ezekből a kifejezésekből az következik, hogy mikor r=rm sebességgel, és azonos értéke lesz Vm, és mikor r=r3És r=R nullával egyenlőek lesznek.
A megfelelő kinetikus energiamezők jelenléte radiális tehetetlenségi erők megjelenéséhez vezet, amelyek a szonda csőből és a cső falától az áramlás közepéig irányulnak. Ezek az erők összenyomják az áramlást, és negatív nyomást hoznak létre a cső falán és a szondacső felületén. Ez a nyomás csökkenti a szonda által mért statikus nyomást. A negatív nyomás nagyságát mindkét területen a fentiek szerint az átlagos kinetikus energiasűrűség határozza meg:
(149)
Ez a nyomás a szondacső átmérőjének növekedésével növekszik, mivel nő az áramlási sebesség, melynek értéke az áramlás folytonossági feltételéből adódik:
, (150)
Ahol V- a folyadék áramlási sebessége a szonda által zavartalanul. A (150) kifejezésből a következőket találjuk:
(151)
Így kiderül, hogy a meglévő mérőműszerek nem tudják pontosan mérni a nyomást a folyadékáramban. Ez a körülmény, mint látjuk, magának a nyomásmérési technikának köszönhető.
A folyadékáramlás sebességének és a benne lévő nyomás meghatározásának problémájának elemzése azt mutatja, hogy ennek a problémának nincs elég egyszerű megoldása. Ez mindenekelőtt annak a ténynek köszönhető, hogy a folyadék a szilárd anyaggal ellentétben könnyen megváltoztatja alakját a részecskéi közötti lényegesen kisebb tapadás miatt. És mégis, a tapadási erők elegendőek ahhoz, hogy befolyásolják a folyadék teljes térfogatának mozgását mind a hidraulikus rendszerben, mind azon kívül. Így például egy táguló kúpos fúvókánál a folyadékáramlás megnő, azaz. az edényből való kiáramlásának sebessége megnő. Ez a jelenség csak a lehulló folyadék tömegének növekedésével és ennek következtében a járulékos nyomás növekedésével magyarázható. Ezért a hidraulikus rendszerben és azon kívül lévő folyadékot egyetlen testnek kell tekinteni, amely a rendszer különböző részein eltérő alakváltozásoknak van kitéve.
A fentiek fényében felmerül a kérdés a maga Daniel Bernoulli által kapott egyenlet fizikai lényegével kapcsolatban.
Lényegének tisztázására térjünk rá erre az egyenletre a (8) kifejezés formájában. Itt p1És p2 statikus és és dinamikus nyomások. Ebből az egyenletből az következik, hogy a statikus és dinamikus nyomások összege, i.e. a teljes nyomás állandó érték egy elemi áramcső teljes hosszában. Ez az állítás azonban csak egy feltétel mellett lesz igaz – nyomás alatt p2, amint fentebb bemutattuk, nem a folyadék kilökött részéből eredő ellennyomást kell érteni, amelyet -ként jelöltünk, hanem a vizsgált folyadékszakasz áramlási nyomását. Bernoulli törvényében ezt a feltételt nem részletezi, sőt nem is sejteti.
A Bernoulli-törvény lényegét másképp is meg lehet kommentálni. A statikus nyomás az energiamegmaradás törvényének megfelelően, amikor egy folyadék mozog, a dinamikus nyomás mértékével kell csökkennie, bár valójában a folyadékáramlásban nincs dinamikus nyomás, mivel a kifejezés csak valódi nyomásként jelenik meg. amikor a teljes áramlás vagy annak egy része lelassul . Valójában a kifejezés a térfogati kinetikus energiasűrűség, azaz. az egységnyi mozgó folyadék térfogatára jutó mozgási energia mennyisége. Valójában ez a kifejezés a statikus nyomás elvesztését jelenti annak mozgási energiává való átalakulása miatt. Ezért ha statikus nyomásra megyünk R nyomásveszteséget adunk hozzá, majd visszatérünk az eredeti statikus nyomáshoz, ami folyadékmozgás hiányában következne be. Tehát a nyomás p1 a Bernoulli-egyenletben valójában az eredeti nyomásnál kisebb nyomás van p1. Ugyanez mondható el a második szakasz nyomásairól. Ez a körülmény azonban szintén nincs megadva az egyenlet levezetésénél. Ha tehát az áramlás első és második szakaszában a nyomásokhoz hozzáadjuk a folyadékmozgásból adódó megfelelő nyomásveszteségeket, akkor a (8) egyenlet alapján azt mondhatjuk, hogy a kezdeti statikus nyomás mindkét szakaszban folyadékmozgás hiányában. ugyanaz volt. Lényegében ez a kezdeti hidrosztatikus nyomás állandóságának törvénye, azaz. ez a Pascal-törvény analógja egy mozgó folyadékra.
Van egy másik mód is a Bernoulli-törvény fizikai lényegének magyarázatára. Korábban már megjegyeztük, hogy a kifejezés egy mozgó folyadék kinetikus energiájának térfogati sűrűségét jelenti. Nyilvánvalóan ugyanez mondható el a statikus nyomásról is R, ami szintén energiasűrűségnek tekinthető, de nem kinetikai, hanem potenciális. A súlynyomással kapcsolatban rgH, akkor a folyadék tömegének potenciális energiasűrűségének is tekinthető. Ezért Bernoulli törvénye a térfogati energiasűrűség megmaradásának törvényeként is értelmezhető, i.e. az egységnyi folyadék térfogatára jutó energia megmaradásának törvénye.
Így a Bernoulli-törvény elemzése azt mutatja, hogy nagyon szigorú fizikai jelentése van, amely az energia megmaradás törvényéhez kapcsolódik. A Bernoulli-egyenlet azonban nem használható közvetlenül a folyadékáramlási sebességek ismert nyomásokból történő meghatározására, vagy fordítva, még ideális folyadék esetén sem, mivel nem veszi figyelembe a külső ellenállást és az ellenállást az áramlás szűkítő szakaszában. Az egyenlet levezetésekor az erők munkáját hibásan számították ki, mivel mindegyiket az első szakaszra kellett csökkenteni, és ezért megszorozni az elmozdulással Dl1. A Bernoulli-egyenlet használata a sebességek vagy nyomások meghatározására jelentős hibákhoz vezet. A Toricelli-képlet használata egy tetszőleges lyukból történő folyadékáramlás sebességének meghatározására szintén illegális, mivel ebben az esetben szó sincs szabadesésről.
Következésképpen a Bernoulli-törvényt fennállása során félreértették, valójában a mechanika egyik mítosza, de segítségével kiderült, hogy a mozgó folyadékban szinte minden hidrodinamikai jelenséget (hatást) meg lehet magyarázni. És meglepő módon ez a lehetőség az egyenlet levezetése során elkövetett hibák miatt adódott. Történt ugyanis, hogy az egyenlet levezetésekor a nyomóerőkből származó minden munka csak egyenlő térfogatú, r tömegű folyadék mozgási energiájának megváltoztatására ment. m, aminek eredményeként egy fizikailag értelmes eredmény született, amely lényegében a potenciális energia mozgási energiává történő átalakulásából, és ennek következtében ezen energiák összegének állandóságából áll a folyadékáramlás minden szakaszában.
A Bernoulli-törvény félreértését az is elősegítette, hogy a mozgó folyadékban hiányzik a kinetikus energiamező fogalma és az ezzel járó gradiens.
Összegzésképpen emlékeztetni kell arra, hogy az általunk kapott képletek csak hozzávetőlegesen használhatók a folyadékáramláson belüli sebességek és nyomások kiszámítására, mivel a külső nyomás a folyadékrészecskékre ható kohéziós erők hatása miatt nem állapítható meg pontosan.

Bernoulli-féle differenciálegyenlet a következő alakú egyenlet:
, ahol n ≠ 0 , n ≠ 1 , p és q x függvényei.

Bernoulli differenciálegyenlet megoldása lineáris egyenletre redukálással

Tekintsük a Bernoulli differenciálegyenletet:
(1) ,
ahol n ≠ 0 , n ≠ 1 , p és q x függvényei.
Osszuk el y n-nel. Amikor y ≠ 0 vagy n< 0 nekünk van:
(2) .
Ez az egyenlet lineáris egyenletté redukálható a változó megváltoztatásával:
.
Mutassuk meg. A komplex függvény differenciálási szabálya szerint:
;
.
Cseréljük be (2) és átalakítjuk:
;
.
Ez egy lineáris, z-hez viszonyított differenciálegyenlet. Megoldása után n >-re 0 , akkor az y = esetet kell figyelembe vennünk 0 . Amikor n > 0 , y = 0 egyben megoldása is az egyenletnek (1) és szerepelnie kell a válaszban.

Megoldás Bernoulli módszerrel

A kérdéses egyenlet (1) Bernoulli módszerével is megoldható. Ehhez keresünk megoldást az eredeti egyenletre két függvény szorzata formájában:
y = u·v ,
ahol u és v x függvényei. Differenciálj x-hez képest:
y′ = u′ v + u v′ .
Helyettesítsd be az eredeti egyenletbe (1) :
;
(3) .
V-ként felvesszük az egyenlet bármely nem nulla megoldását:
(4) .
Az egyenlet (4) egy elválasztható változókat tartalmazó egyenlet. Megoldjuk, és találunk egy adott megoldást v = v (x). Egy adott megoldást helyettesítünk (3) . Mivel kielégíti az egyenletet (4) , akkor a zárójelben lévő kifejezés nulla lesz. Kapunk:
;
.
Itt v x egy már ismert függvénye. Ez egy elválasztható változókkal rendelkező egyenlet. Megtaláljuk általános megoldását, és vele együtt az eredeti y = uv egyenlet megoldását is.

Példa a Bernoulli-differenciálegyenlet megoldására

Oldja meg az egyenletet

Megoldás

Első pillantásra úgy tűnik, hogy ez a differenciálegyenlet nem hasonlít a Bernoulli-egyenlethez. Ha x-et tekintjük független változónak, y-t függő változónak (vagyis ha y x függvénye), akkor ez igaz. De ha y-t tekintjük független változónak és x-et függő változónak, akkor könnyen belátható, hogy ez Bernoulli egyenlete.

Tehát feltételezzük, hogy x az y függvénye. Helyettesítsük be és szorozzuk meg:
;
;
(1. o.) .
Ez a Bernoulli-egyenlet n =-vel 2 . Ez eltér a fent tárgyalt egyenlettől (1) , csak a változók jelölésével (x helyett y). Bernoulli módszerével oldjuk meg. Csináljunk egy cserét:
x = u v ,
ahol u és v y függvényei. Különbségtétel y szerint:
.
Cseréljük be (1. o.):
;
(2. o.) .
Bármilyen nem nulla függvényt keresünk v (y), kielégítve a következő egyenletet:
(3. o.) .
Különválasztjuk a változókat:
;
;
.
Legyen C = 0 , mivel az egyenletre bármilyen megoldásra van szükségünk (3. o.).
;
.
Cseréljük be (2. o.) figyelembe véve, hogy a zárójelben lévő kifejezés nullával egyenlő (ami miatt (3. o.)):
;
;
.
Válasszuk szét a változókat. Amikor u ≠ 0 nekünk van:
;
(4. o.) ;
.
A második integrálban végrehajtjuk a helyettesítést:
;
.

Bernoulli egyenlet én Bernoulli egyenlet

A forma elsőrendű differenciálegyenlete:

dy/dx + Py = Qy α ,

Ahol P, Q- adott folyamatos függvények től x; α - állandó szám. Új funkció bevezetése z = y --α+1 B. u. lineáris differenciálegyenletté redukálódik (Lásd Lineáris differenciálegyenletek) tekintetében z. Lehurrogás. J. Bernoulli 1695-ben vette figyelembe, a megoldási módszert J. Bernoulli publikálta 1697-ben.

II Bernoulli egyenlet

a hidrodinamika alapegyenlete (lásd: Hidrodinamika) , viszonyítva (az egyenletes áramláshoz) az áramló folyadék sebességéhez v, nyomás benne Rés magasság h kis mennyiségű folyadék elhelyezkedése a referenciasík felett. Lehurrogás. D. Bernoulli származtatta 1738-ban a ρ állandó sűrűségű ideális összenyomhatatlan folyadékáramra, amely csak a gravitáció hatása alatt áll. Ebben az esetben B. at. a következő formában van:

v 2 / 2 + plρ + gh= állandó,

Ahol g- a gravitáció gyorsulása. Ha ezt az egyenletet megszorozzuk ρ-vel , akkor az 1. tag egységnyi térfogatú folyadék mozgási energiáját jelenti, a másik 2 tag pedig a potenciális energiát, aminek egy része a gravitációnak köszönhető (az egyenlet utolsó tagja), a másik része pedig nyomás p. Lehurrogás. ebben a formában az energiamegmaradás törvényét fejezi ki. Ha egyfajta energia, például kinetikus, nő a folyadékáram mentén, akkor a potenciális energia ugyanennyivel csökken. Ezért például a csővezetéken átfolyó áramlás szűkülésekor, az áramlási sebesség növekedésével (mivel ugyanannyi folyadék halad át kisebb keresztmetszeten ugyanannyi idő alatt, mint nagyobb keresztmetszeten), a benne lévő nyomás ennek megfelelően csökken (ez a Venturi áramlásmérő működési elvén alapul).

A B. u. Ebből számos fontos következmény következik. Például amikor a gravitáció hatására egy folyadék áramlik egy nyitott edényből ( rizs. 1 ) B.-tól at. következik:

v 2 /2g = h vagy

azaz a folyadék sebessége a kimenetben megegyezik azzal, amikor a folyadékrészecskék szabadon esnek a magasból h.

Ha egyenletes folyadékáramlás van, amelynek sebessége v 0 és nyomása p 0 , akadályba ütközik útközben ( rizs. 2 ), akkor közvetlenül az akadály előtt van egy tartalék - az áramlás lassulása; a holtág közepén, a kritikus ponton az áramlási sebesség nulla. A B. u. ebből következik, hogy a nyomás a kritikus pontban p 1 = p 0 + ρ v 2 0 /2. A nyomásnövekmény ezen a ponton egyenlő p 1 -o 0 = ρ v A 2 0 /2-t dinamikus nyomásnak vagy sebességnyomásnak nevezzük. Valódi folyadékáramban mechanikai energiája nem marad meg az áramlás mentén, hanem a súrlódási erők munkájára fordítódik, és hőenergia formájában disszipálódik, ezért biodinamikus folyadék használatakor. Valódi folyadék esetén figyelembe kell venni az ellenállási veszteségeket.

Lehurrogás. nagy jelentősége van a hidraulikában (Lásd Hidraulika) és a műszaki hidrodinamikában: használják csővezetékek, szivattyúk számításaiban, szűréssel kapcsolatos kérdések megoldásában stb. Bernoulli-egyenlet változó sűrűségű közeghez R a tömegváltozatlanság egyenletével és az állapotegyenlettel együtt a gázdinamika alapja (lásd Gázdinamika).

Megvilágított.: Fabrikant N.Ya., Aerodinamika, 1-2. rész, L., 1949-64; Uginchus A. A., Hidraulika, hidraulikus gépek és a mezőgazdasági vízellátás alapjai, K.-M., 1957, ch. V.

Nagy Szovjet Enciklopédia. - M.: Szovjet Enciklopédia. 1969-1978 .

Nézze meg, mi a „Bernoulli-egyenlet” más szótárakban:

- (Bernoulli integrál) a hidroaeromechanikában (D. Bernoulli svájci tudósról nevezték el), az egyik fő. hidromechanikai egyenletek, amelyek egy összenyomhatatlan ideális folyadék egyenletes mozgása során egyenletes gravitációs térben a következő alakúak: ahol v... ... Fizikai enciklopédia

Ideális összenyomhatatlan folyadék áramlásának sebességét és nyomását állítja össze egyenletes áramlás mellett. A Bernoulli-egyenlet egy mozgó folyadék energiamegmaradásának törvényét fejezi ki. Széles körben használják a hidraulikában és a műszaki folyadékdinamikában. Származta: D....... Nagy enciklopédikus szótár

Az aerodinamikában és a hidrodinamikában a gázt vagy a hidrodinamikai változókat egy ideális folyadék vagy gáz állandó barotrop áramlásának áramvonala mentén összekötő kapcsolat a tömegerők potenciálterében F = grad(Π), ahol (Π) potenciál: (Π) + V2/2 + … Technológia enciklopédiája

Ideális összenyomhatatlan folyadék áramlásának sebességét és nyomását állítja össze egyenletes áramlás mellett. A Bernoulli-egyenlet egy mozgó folyadék energiamegmaradásának törvényét fejezi ki. Széles körben használják a hidraulikában és a műszaki folyadékdinamikában. Kimenet... ... enciklopédikus szótár

I. rendű közönséges differenciálegyenlet ahol. egy valós szám, amely nem egyenlő nullával vagy eggyel. Ezt az egyenletet először J. Bernoulli vette figyelembe. A B. u. elsőrendű lineáris inhomogén egyenletté redukálódik (lásd... ... Matematikai Enciklopédia

Bernoulli egyenlet Enciklopédia "Repülés"

Bernoulli egyenlet- az aero- és hidrodinamikában egy kapcsolat, amely gáz- vagy hidrodinamikai változókat köt össze egy ideális folyadék vagy gáz állandó barotróp [ρ = ρ(p)] áramlásának áramvonala mentén a tömegerők potenciális mezőjében (F = -gradΠ, ahol Π … … Enciklopédia "Repülés"

- [a svájciakról nevezték el. tudós D. Bernoulli (1700 1782)] az egyik fő. hidrodinamikai egyenlet, kifejezve az energia megmaradás törvényét. 1) B. at. elemi (kis keresztmetszetű) ideális folyadékáramhoz: ahol p, PO és v statikus... ... Nagy enciklopédikus politechnikai szótár

Ideális összenyomhatatlan folyadék áramlásának sebességét és nyomását állítja össze egyenletes áramlás mellett. Lehurrogás. egy mozgó folyadék energiamegmaradásának törvényét fejezi ki. Széles körben használják a hidraulikában és a technológiában. hidrodinamika. D. Bernoulli fejlesztette ki 1738-ban... Természettudomány. enciklopédikus szótár

Bernoulli-egyenlet, a hidrodinamika alapegyenlete, amely összeköti (egyenletes áramláshoz) az áramló folyadék sebességét v, a benne lévő nyomást p és a kis térfogatú folyadék referenciasík feletti elhelyezkedésének h magasságát. Lehurrogás. D. Bernoulli fejlesztette ki a... Nagy Szovjet Enciklopédia

Könyvek

• Hidrodinamika, avagy jegyzetek a folyadékok erőiről és mozgásairól, D. Bernoulli. Ez a könyv az Ön megrendelésének megfelelően, igény szerinti nyomtatás technológiával készül. 1738-ban Daniel Bernoulli híres műve, a „Hidrodinamika, avagy Megjegyzések az erőkről és...