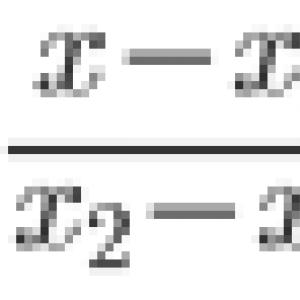
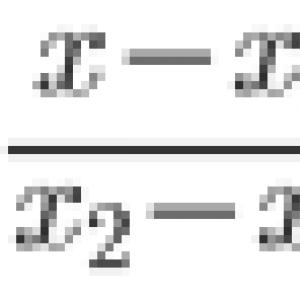
Lagrange-módszer (állandó variációja). Elsőrendű lineáris differenciálegyenletek

Tekintsünk egy elsőrendű lineáris inhomogén differenciálegyenletet:
(1) .
Az egyenlet megoldásának három módja van:

• állandó variációs módszere (Lagrange).

Tekintsük egy elsőrendű lineáris differenciálegyenlet megoldását a Lagrange-módszerrel.

Az állandó változásának módszere (Lagrange)

A konstans módszer variációjában az egyenletet két lépésben oldjuk meg. Első lépésben egyszerűsítjük az eredeti egyenletet, és megoldunk egy homogén egyenletet. A második szakaszban a megoldás első szakaszában kapott integrációs állandót egy függvényre cseréljük. Ezután általános megoldást keresünk az eredeti egyenletre.

Tekintsük az egyenletet:
(1)

1. lépés Homogén egyenlet megoldása

A homogén egyenletre keresünk megoldást:

Ez egy elválasztható egyenlet

Elválasztjuk a változókat - szorozzuk dx-el, osztjuk y-vel:

Integráljunk:

Integrál y felett - táblázatos:

Akkor

Potencírozzuk:

Cseréljük ki az e C állandót C-re, és távolítsuk el a modulusjelet, ami egy konstans szorzásából adódik. ±1, amelyet a C-be foglalunk:

2. lépés Cserélje ki a C állandót a függvényre

Most cseréljük le a C állandót x függvényére:
C → u (x)
Vagyis megoldást fogunk keresni az eredeti egyenletre (1) mint:
(2)
A származék megkeresése.

A komplex függvény differenciálási szabálya szerint:
.
A termékdifferenciálási szabály szerint:

.
Helyettesítsd be az eredeti egyenletbe (1) :
(1) ;

.
Két tag csökken:
;
.
Integráljunk:
.
Csere be (2) :
.
Ennek eredményeként általános megoldást kapunk egy elsőrendű lineáris differenciálegyenletre:
.

Példa elsőrendű lineáris differenciálegyenlet megoldására Lagrange módszerrel

Oldja meg az egyenletet

Megoldás

Megoldjuk a homogén egyenletet:

Különválasztjuk a változókat:

Szorozva:

Integráljunk:

Táblázatos integrálok:

Potencírozzuk:

Cseréljük ki az e C állandót C-re, és távolítsuk el a modulusjeleket:

Innen:

Cseréljük le a C állandót x függvényével:
C → u (x)

A származék megkeresése:
.
Helyettesítsd be az eredeti egyenletbe:
;
;
Vagy:
;
.
Integráljunk:
;
Az egyenlet megoldása:
.

Az elsőrendű lineáris differenciálegyenletek és a Bernoulli-egyenlet megoldásának másik módja egy tetszőleges állandó variációs módszere, vagy a Lagrange-módszer.

Az elsőrendű lineáris differenciálegyenletek y’+p(x)y=q(x) alakú egyenletek. Ha a jobb oldalon van egy nulla: y’+p(x)y=0, akkor ez egy lineáris homogén 1. rendű egyenlet. Ennek megfelelően egy egyenlet, amelynek jobb oldala nem nulla, y’+p(x)y=q(x) heterogén 1. rendű lineáris egyenlet.

Egy tetszőleges állandó változtatásának módszere (Lagrange-módszer) az alábbiak:

1) Általános megoldást keresünk az y’+p(x)y=0 homogén egyenletre: y=y*.

2) Az általános megoldásban C-t nem állandónak, hanem x függvényének tekintjük: C = C (x). Megkeressük az (y*)’ általános megoldás deriváltját, és a kapott kifejezést y*-ra és (y*)’-re behelyettesítjük a kezdeti feltételbe. A kapott egyenletből megtaláljuk a C(x) függvényt.

3) A homogén egyenlet általános megoldásában C helyett a talált C(x) kifejezést helyettesítjük.

Nézzünk példákat egy tetszőleges állandó változtatásának módszerére. Vegyük ugyanazokat a feladatokat, mint itt, hasonlítsuk össze a megoldás előrehaladását, és győződjön meg arról, hogy a kapott válaszok egybeesnek.

1) y’=3x-y/x

Írjuk át az egyenletet szabványos formában (ellentétben Bernoulli módszerével, ahol csak azért volt szükségünk a jelölési formára, hogy lássuk, hogy az egyenlet lineáris).

y’+y/x=3x (I). Most a terv szerint haladunk.

1) Oldja meg az y’+y/x=0 homogén egyenletet! Ez egy elválasztható változókkal rendelkező egyenlet. Képzelje el, hogy y’=dy/dx, helyettesítse: dy/dx+y/x=0, dy/dx=-y/x. Az egyenlet mindkét oldalát megszorozzuk dx-el, és elosztjuk xy≠0-val: dy/y=-dx/x. Integráljunk:

2) A homogén egyenlet így kapott általános megoldásában C-t nem állandónak, hanem x függvényének fogjuk tekinteni: C=C(x). Innen

A kapott kifejezéseket behelyettesítjük az (I) feltételbe:

Integráljuk az egyenlet mindkét oldalát:

itt C már valami új állandó.

3) Az y=C/x homogén egyenlet általános megoldásában, ahol C=C(x), azaz y=C(x)/x-et feltételeztünk, C(x) helyett a talált x³ kifejezést helyettesítjük. +C: y=(x³ +C)/x vagy y=x²+C/x. Ugyanazt a választ kaptuk, mint a Bernoulli-féle megoldásnál.

Válasz: y=x²+C/x.

2) y’+y=cosx.

Itt az egyenlet már szabványos formában fel van írva, nem kell átalakítani.

1) Oldja meg az y’+y=0 homogén lineáris egyenletet: dy/dx=-y; dy/y=-dx. Integráljunk:

A kényelmesebb jelölési forma érdekében a kitevőt C hatványára vesszük, mint új C-t:

Ezt a transzformációt azért hajtottuk végre, hogy kényelmesebb legyen a derivált megtalálása.

2) A lineáris homogén egyenlet így kapott általános megoldásában C-t nem állandónak, hanem x függvényének tekintjük: C=C(x). Ilyen feltételek mellett

A kapott y és y' kifejezéseket behelyettesítjük a feltételbe:

Szorozzuk meg az egyenlet mindkét oldalát ezzel

Az egyenlet mindkét oldalát a részenkénti integráció képlet segítségével integráljuk, így kapjuk:

Itt C már nem függvény, hanem közönséges konstans.

3) A homogén egyenlet általános megoldásában

helyettesítse be a talált C(x) függvényt:

Ugyanazt a választ kaptuk, mint a Bernoulli-féle megoldásnál.

Egy tetszőleges állandó változtatásának módszere is alkalmazható megoldásra.

y'x+y=-xy².

Az egyenletet szabványos alakba hozzuk: y’+y/x=-y² (II).

1) Oldja meg az y’+y/x=0 homogén egyenletet! dy/dx=-y/x. Az egyenlet mindkét oldalát megszorozzuk dx-el és elosztjuk y-vel: dy/y=-dx/x. Most integráljuk:

A kapott kifejezéseket behelyettesítjük a (II) feltételbe:

Egyszerűsítsünk:

Kaptunk egy egyenletet elválasztható változókkal C és x esetén:

Itt C már egy közönséges állandó. Az integrálás során a C(x) helyett egyszerűen C-t írtunk, hogy ne terheljük túl a jelölést. És a végén visszatértünk C(x)-hez, hogy ne keverjük össze C(x)-et az új C-vel.

3) Az y=C(x)/x homogén egyenlet általános megoldásában behelyettesítjük a talált C(x) függvényt:

Ugyanazt a választ kaptuk, mint amikor Bernoulli módszerrel oldottuk meg.

Példák öntesztre:

1. Írjuk át az egyenletet szabványos formában: y’-2y=x.

1) Oldja meg az y’-2y=0 homogén egyenletet! y’=dy/dx, tehát dy/dx=2y, szorozd meg az egyenlet mindkét oldalát dx-el, oszd el y-vel és integráld:

Innen találjuk y:

Az y és y’ kifejezéseket behelyettesítjük a feltételbe (a rövidség kedvéért C-t használunk C(x) helyett és C'-t C"(x) helyett):

A jobb oldali integrál megtalálásához a részenkénti integráció képletet használjuk:

Most behelyettesítjük az u, du és v karaktereket a képletbe:

Itt C =konst.

3) Most homogénnel helyettesítjük az oldatot

Tetszőleges állandók változtatásának módszere

Tetszőleges állandók variációs módszere lineáris inhomogén differenciálegyenlet megoldásának megalkotásához

a n (t)z (n) (t) + a n − 1 (t)z (n − 1) (t) + ... + a 1 (t)z"(t) + a 0 (t)z(t) = f(t)

tetszőleges állandók cseréjéből áll c k az általános megoldásban

z(t) = c 1 z 1 (t) + c 2 z 2 (t) + ... + c n z n (t)

megfelelő homogén egyenlet

a n (t)z (n) (t) + a n − 1 (t)z (n − 1) (t) + ... + a 1 (t)z"(t) + a 0 (t)z(t) = 0

segédfunkciókhoz c k (t) , melynek deriváltjai kielégítik a lineáris algebrai rendszert

Az (1) rendszer meghatározója az Wronskian funkciókat z 1 ,z 2 ,...,z n , amely biztosítja annak egyedi megoldhatóságát tekintetében.

Ha az integrációs állandók fix értékein vett antideriválták, akkor a függvény

megoldása az eredeti lineáris inhomogén differenciálegyenletre. Egy inhomogén egyenlet integrálása általános megoldás jelenlétében a megfelelő homogén egyenletre így redukálódik kvadratúrák.

Tetszőleges állandók variációs módszere lineáris differenciálegyenlet-rendszer megoldásainak megalkotására vektor normál formában

egy adott megoldás (1) megalkotásából áll a formában

Ahol Z(t) a megfelelő homogén egyenlet megoldásainak alapja, mátrix formájában felírva, és a tetszőleges állandók vektorát helyettesítő vektorfüggvényt a reláció határozza meg. A szükséges konkrét megoldás (nulla kezdeti értékkel a t = t 0 úgy néz ki

Egy állandó együtthatójú rendszer esetén az utolsó kifejezés leegyszerűsödik:

Mátrix Z(t)Z− 1 (τ) hívott Cauchy mátrix operátor L = A(t) .

Külső linkek

• exponenta.ru - Elméleti információk példákkal

Wikimédia Alapítvány. 2010.