Az f x függvényt párosnak nevezzük. A függvény főbb tulajdonságai: páros, páratlan, periodicitás, korlátosság

A páros és páratlan függvények az egyik fő tulajdonsága, és a paritás a matematika iskolai kurzusának lenyűgöző részét foglalja el. Nagymértékben meghatározza a függvény viselkedésének jellegét, és nagyban megkönnyíti a megfelelő gráf felépítését.

Határozzuk meg a függvény paritását. Általánosságban elmondható, hogy a vizsgált függvényt akkor is figyelembe kell venni, ha a tartományában található független változó (x) ellentétes értékei esetén az y (függvény) megfelelő értékei egyenlőek.

Adjunk egy szigorúbb definíciót. Tekintsünk néhány f (x) függvényt, amely a D tartományban van definiálva. Ez akkor is így lesz, ha bármely, a definíciós tartományban található x pontra:

• -x (ellentétes pont) is az adott hatókörbe tartozik,

• f(-x) = f(x).

A fenti definícióból egy ilyen függvény definíciós tartományához szükséges feltétel következik, nevezetesen a szimmetria a koordináták origójának számító O ponthoz képest, hiszen ha valamely b pont egy függvény definíciós tartományában található. páros függvény, akkor a megfelelő - b pont is ebben a tartományban található. A fentiekből tehát a következő következtetés vonható le: páros funkció szimmetrikus az y tengelyhez képest (Oy).

Hogyan határozzuk meg egy függvény paritását a gyakorlatban?

Adjuk meg a h(x)=11^x+11^(-x) képlettel. A definícióból közvetlenül következő algoritmust követve mindenekelőtt annak definíciós területét vizsgáljuk. Nyilvánvalóan az argumentum összes értékére definiálva van, vagyis az első feltétel teljesül.

A következő lépés az (x) argumentum behelyettesítése az ellenkező értékével (-x).
Kapunk:
h(-x) = 11^(-x) + 11^x.
Mivel az összeadás teljesíti a kommutatív (eltolódási) törvényt, nyilvánvaló, hogy h(-x) = h(x) és az adott funkcionális függés páros.

Ellenőrizzük a h(x)=11^x-11^(-x) függvény egyenletességét. Ugyanezt az algoritmust követve h(-x) = 11^(-x) -11^x kapjuk. Kivéve a mínuszt, ennek eredményeként megvan
h(-x)=-(11^x-11^(-x))=- h(x). Ezért h(x) páratlan.

Egyébként emlékeztetni kell arra, hogy vannak olyan függvények, amelyeket nem lehet e szempontok szerint besorolni, nem nevezik sem párosnak, sem páratlannak.

Még a függvényeknek is van számos érdekes tulajdonsága:

• hasonló függvények hozzáadása eredményeként egy párost kapunk;
• az ilyen függvények kivonása eredményeképpen egy párost kapunk;
• páros, szintén páros;
• két ilyen függvény szorzásának eredményeként egy párost kapunk;
• a páratlan és páros függvények szorzásának eredményeként páratlant kapunk;
• a páratlan és páros függvények felosztása eredményeként egy páratlant kapunk;
• egy ilyen függvény deriváltja páratlan;
• Ha egy páratlan függvényt négyzetre emelünk, akkor párost kapunk.

Egy függvény paritása felhasználható egyenletek megoldásában.

Egy olyan egyenlet megoldásához, mint a g(x) = 0, ahol az egyenlet bal oldala páros függvény, elég lesz megoldást találni a változó nemnegatív értékeire. Az egyenlet kapott gyökeit ellentétes számokkal kell kombinálni. Egyikük ellenőrzés alatt áll.

Ugyanezt sikeresen alkalmazták a megoldásra nem szabványos feladatok paraméterrel.

Például van-e olyan értéke az a paraméternek, amely miatt a 2x^6-x^4-ax^2=1 egyenletnek három gyöke lenne?

Ha figyelembe vesszük, hogy a változó páros hatványokban lép be az egyenletbe, akkor egyértelmű, hogy az x -x-re cserélése nem változtatja meg az adott egyenletet. Ebből következik, hogy ha egy bizonyos szám a gyöke, akkor az ellenkező szám is. A következtetés nyilvánvaló: az egyenlet nullától eltérő gyökerei „párokban” szerepelnek a megoldások halmazában.

Nyilvánvaló, hogy maga a 0 nem az, vagyis egy ilyen egyenlet gyökeinek száma csak páros lehet, és természetesen a paraméter egyetlen értékére sem lehet három gyöke.

De a 2^x+ 2^(-x)=ax^4+2x^2+2 egyenlet gyökeinek száma páratlan lehet, és a paraméter bármely értékére. Valóban, könnyen ellenőrizhető, hogy egy adott egyenlet gyökhalmaza "párokban" tartalmaz-e megoldásokat. Ellenőrizzük, hogy a 0 gyökér-e. Ha behelyettesítjük az egyenletbe, 2=2-t kapunk. Így a "páros" mellett a 0 egy gyök is, ami a páratlan számukat bizonyítja.

Funkciókutatás.

1) D(y) - Definíciós tartomány: az x változó összes értékének halmaza. amely alatt az f(x) és g(x) algebrai kifejezéseknek van értelme.

Ha a függvényt egy képlet adja meg, akkor a definíciós tartomány a független változó összes olyan értékéből áll, amelyre a képletnek van értelme.

2) A függvény tulajdonságai: páros/páratlan, periodicitás:

páratlanÉs még függvényeknek nevezzük, amelyek grafikonjai szimmetrikusak az argumentum előjelének változására vonatkozóan.

páratlan függvény- függvény, amely a független változó előjelének megváltozásakor az értéket az ellenkezőjére változtatja (a koordináták középpontjára szimmetrikusan).

Egyenletes funkció- olyan függvény, amely nem változtatja meg értékét a független változó előjelének megváltozásakor (szimmetrikus az y tengelyre).

Se nem páros, se nem páratlan függvény (általános funkció) olyan függvény, amelynek nincs szimmetriája. Ez a kategória olyan funkciókat tartalmaz, amelyek nem tartoznak az előző 2 kategóriába.

A fenti kategóriák egyikébe sem tartozó függvényeket hívjuk meg se páros, se nem páratlan(vagy általános függvények).

Páratlan függvények

Egy páratlan hatvány ahol egy tetszőleges egész szám.

Egyenletes funkciókat

Páros hatvány ahol egy tetszőleges egész szám.

Periodikus funkció egy olyan függvény, amely megismétli az értékeit az argumentum bizonyos szabályos intervallumában, azaz nem változtatja meg az értékét, ha valamilyen rögzített nullától eltérő számot adunk az argumentumhoz ( időszak függvények) a teljes definíciós tartományban.

3) A függvény nullái (gyökei) azok a pontok, ahol eltűnik.

A grafikon és a tengely metszéspontjának megtalálása Oy. Ehhez ki kell számítania az értéket f(0). Keresse meg a grafikon és a tengely metszéspontjait is Ökör, miért kell megtalálni az egyenlet gyökereit f(x) = 0 (vagy győződjön meg arról, hogy nincsenek gyökök).

Azokat a pontokat, ahol a gráf metszi a tengelyt, nevezzük függvény nullák. A függvény nulláinak megtalálásához meg kell oldani az egyenletet, vagyis meg kell találni azok az x értékek, amelynél a függvény eltűnik.

4) A jelek állandóságának intervallumai, a bennük lévő jelek.

Intervallumok, ahol az f(x) függvény megtartja előjelét.

Az állandósági intervallum az intervallum minden ponton, ahol függvény pozitív vagy negatív.

Az x tengely felett.

tengely ALATT.

5) Folytonosság (a folytonossági pontok, a folytonossági jelleg, aszimptoták).

folyamatos funkció- „ugrások” nélküli függvény, vagyis olyan, amelyben az argumentum kis változtatásai kis mértékben változnak a függvény értékében.

Kivehető töréspontok

Ha a függvény határa létezik, de a függvény ezen a ponton nincs definiálva, vagy a határérték nem egyezik a függvény értékével ezen a ponton:

,

akkor a pontot nevezik töréspont függvények (komplex elemzésben eltávolítható szinguláris pont).

Ha "javítjuk" a függvényt egy eltávolítható folytonossági hiány pontján és helyezzük el , akkor egy olyan függvényt kapunk, amely ezen a ponton folytonos. Egy függvény ilyen műveletét ún a funkció kiterjesztése folyamatosra vagy a funkció kiterjesztése folytonosság által, ami a pont nevét indokolja, pontként egyszer használatos rés.

Az első és a második típusú megszakítási pontok

Ha a függvénynek egy adott pontban megszakadása van (azaz egy adott pontban a függvény határértéke hiányzik, vagy nem esik egybe a függvény adott pontban lévő értékével), akkor numerikus függvényekre két lehetőség van. numerikus függvények létezésével kapcsolatos egyoldalú korlátok:

ha mindkét egyoldalú határérték létezik és véges, akkor egy ilyen pontot nevezünk az első fajtájú töréspont. Az eltávolítható megszakítási pontok az első típusú szakadási pontok;

ha az egyoldali határértékek közül legalább az egyik nem létezik, vagy nem véges érték, akkor egy ilyen pontot ún. a második típusú töréspont.

Aszimptota - egyenes, amelynek az a tulajdonsága, hogy a görbe egy pontjától mért távolság ez egyenes nullára hajlik, ahogy a pont az ág mentén a végtelenbe mozog.

függőleges

Függőleges aszimptota - határvonal .

A függőleges aszimptota meghatározásakor általában nem egy határt, hanem két egyoldalút (bal és jobb) keresnek. Ennek célja annak meghatározása, hogy a függvény hogyan viselkedik, amikor különböző irányokból megközelíti a függőleges aszimptotát. Például:

Vízszintes

Vízszintes aszimptota - egyenes fajok, a létezés függvényében határ

.

ferde

Ferde aszimptota - egyenes fajok, a létezés függvényében határait

Megjegyzés: Egy függvénynek legfeljebb két ferde (vízszintes) aszimptotája lehet.

Megjegyzés: ha a fent említett két határérték közül legalább az egyik nem létezik (vagy egyenlő azzal), akkor a (vagy ) pontban lévő ferde aszimptóta nem létezik.

ha a 2.), akkor , és a határértéket a vízszintes aszimptota képlet határozza meg, .

6) A monotonitás intervallumainak megtalálása. Keresse meg egy függvény monotonitási intervallumát f(x) (azaz növekedési és csökkenési időközök). Ez a származék előjelének vizsgálatával történik f(x). Ehhez keresse meg a származékot f(x) és oldja meg az egyenlőtlenséget f(x)0. Azokon az intervallumokon, ahol ez az egyenlőtlenség teljesül, a függvény f(x) növekszik. Ahol a fordított egyenlőtlenség érvényesül f(x)0, függvény f(x) csökken.

Lelet helyi extrémum. Ha megtaláltuk a monotonitás intervallumait, azonnal meghatározhatjuk egy lokális szélsőség azon pontjait, ahol a növekedést csökkenés váltja fel, vannak lokális maximumok, és ahol a csökkenést növekedés váltja fel, helyi minimumok. Számítsa ki a függvény értékét ezeken a pontokon! Ha egy függvénynek vannak olyan kritikus pontjai, amelyek nem lokális szélsőpontok, akkor célszerű ezeken a pontokon is kiszámítani a függvény értékét.

Az y = f(x) függvény legnagyobb és legkisebb értékének megkeresése egy szakaszon(folytatás)

1. Keresse meg egy függvény deriváltját: f(x). 2. Keresse meg azokat a pontokat, ahol a derivált nulla: f(x)=0x 1, x 2 ,... 3. Határozza meg a pontok tulajdonjogát x 1 ,x 2 , … szegmens [ a; b]: legyen x 1a;b, de x 2a;b .

Megjelenítés elrejtése

A funkció beállításának módjai

Adjuk meg a függvényt a következő képlettel: y=2x^(2)-3 . Ha bármilyen értéket rendel az x független változóhoz, ezzel a képlettel kiszámíthatja az y függő változó megfelelő értékeit. Például, ha x=-0,5 , akkor a képlet segítségével azt kapjuk, hogy y megfelelő értéke y=2 \cdot (-0,5)^(2)-3=-2,5 .

Az y=2x^(2)-3 képletben az x argumentum által felvett bármely érték esetén csak egy függvényérték számítható ki, amely megfelel ennek. A függvény táblázatként ábrázolható:

x	−2	−1	0	1	2	3
y	−4	−3	−2	−1	0	1

A táblázat segítségével kitalálhatja, hogy a -1 argumentum értékéhez a -3 függvény értéke fog megfelelni; és az x=2 érték y=0-nak felel meg, és így tovább. Azt is fontos tudni, hogy a táblázatban minden argumentumérték csak egy függvényértéknek felel meg.

Grafikonok segítségével több függvény is beállítható. A gráf segítségével megállapítható, hogy a függvény melyik értéke korrelál egy adott x értékkel. Leggyakrabban ez a függvény hozzávetőleges értéke.

Páros és páratlan függvény

A funkció az páros funkció, amikor f(-x)=f(x) bármely x esetén a tartományból. Egy ilyen függvény szimmetrikus lesz az Oy tengelyre.

A funkció az páratlan függvény amikor f(-x)=-f(x) bármely x esetén a tartományban. Egy ilyen függvény szimmetrikus lesz az O (0;0) origóra.

A funkció az nem is, sem páratlanés felhívott általános funkciója amikor nincs szimmetriája a tengely vagy az origó körül.

A következő paritásfüggvényt vizsgáljuk:

f(x)=3x^(3)-7x^(7)

D(f)=(-\infty ; +\infty) szimmetrikus definíciós tartománnyal az origóról. f(-x)= 3 \cdot (-x)^(3)-7 \cdot (-x)^(7)= -3x^(3)+7x^(7)= -(3x^(3)-7x^(7))= -f(x).

Ezért az f(x)=3x^(3)-7x^(7) függvény páratlan.

Periodikus funkció

Az y=f(x) függvényt, amelynek tartományában f(x+T)=f(x-T)=f(x) igaz bármely x-re, az ún. periodikus függvény T \neq 0 periódussal.

A függvény grafikonjának megismétlése az abszcissza tengely bármely szakaszán, amelynek T hosszúsága van.

Azok az intervallumok, ahol a függvény pozitív, azaz f (x) > 0 - az abszcissza tengely szakaszai, amelyek megfelelnek a függvény grafikonjának az abszcissza tengelye feletti pontjainak.

f(x) > 0 be (x_(1); x_(2)) \cup (x_(3); +\infty)

Rések, ahol a függvény negatív, azaz f(x)< 0 - отрезки оси абсцисс, которые отвечают точкам графика функции, лежащих ниже оси абсцисс.

f(x)< 0 на (-\infty; x_(1)) \cup (x_(2); x_(3))

Funkció korlátozás

alulról határolt szokás hívni egy y=f(x), x \in X függvényt, ha létezik olyan A szám, amelyre az f(x) \geq A egyenlőtlenség fennáll bármely x \in X esetén.

Példa egy lent korlátos függvényre: y=\sqrt(1+x^(2)), mivel y=\sqrt(1+x^(2)) \geq 1 bármely x esetén.

felülről határolt egy y=f(x), x \in X függvény akkor hívódik meg, ha létezik olyan B szám, amelyre az f(x) \neq B egyenlőtlenség teljesül bármely x \in X esetén.

Példa az alábbiakban behatárolt függvényre: y=\sqrt(1-x^(2)), x \in [-1;1] mivel y=\sqrt(1+x^(2)) \neq 1 bármely x \in [-1;1] esetén.

Korlátozott szokás hívni egy y=f(x), x \in X függvényt, ha létezik olyan K > 0 szám, amelyre a \left | f(x) \jobbra | \neq K tetszőleges x \in X .

Példa korlátos függvényre: y=\sin x az egész számegyenesen korlátos, mert \bal | \sin x \jobbra | \neq 1.

Növekvő és csökkentő funkció

Olyan függvényről szokás beszélni, amely a vizsgált intervallumon növekszik as funkció növelése amikor x nagyobb értéke az y=f(x) függvény nagyobb értékének felel meg. Innen kiderül, hogy a figyelembe vett intervallumból az x_(1) és x_(2) argumentum két tetszőleges értékét, valamint x_(1) > x_(2) , akkor y(x_(1)) lesz. > y(x_(2)) .

A vizsgált intervallumon csökkenő függvényt nevezzük csökkenő funkció amikor x nagyobb értéke az y(x) függvény kisebb értékének felel meg. Innen kiderül, hogy a figyelembe vett intervallumból az x_(1) és x_(2) argumentum két tetszőleges értékét, valamint x_(1) > x_(2) , akkor y(x_(1)) lesz.< y(x_{2}) .

Funkciógyökerek szokás megnevezni azokat a pontokat, amelyekben az F=y(x) függvény metszi az abszcissza tengelyt (ezeket az y(x)=0 egyenlet megoldása eredményeként kapjuk meg).

a) Ha egy páros függvény x > 0 esetén nő, akkor x esetén csökken< 0

b) Ha egy páros függvény x > 0 esetén csökken, akkor x esetén nő< 0

c) Ha egy páratlan függvény növekszik x > 0 esetén, akkor x esetén is nő< 0

d) Ha egy páratlan függvény x > 0 esetén csökken, akkor x esetén is csökken< 0

A funkció szélsőségei

Funkció minimum pontja y=f(x) szokás hívni egy olyan pontot x=x_(0) , amelyben a szomszédságában más pontok lesznek (kivéve az x=x_(0) pontot), és ezekre az f( x) > f (x_(0)) . y_(min) - a függvény kijelölése a pontban min.

Funkció maximum pontja y=f(x) szokás hívni egy olyan pontot x=x_(0) , amelyben a szomszédságában további pontok lesznek (kivéve az x=x_(0) pontot), majd az f(x) egyenlőtlenséget elégedett lesz velük< f(x^{0}) . y_{max} - обозначение функции в точке max.

Szükséges állapot

Fermat tétele szerint: f"(x)=0, akkor amikor az x_(0) pontban differenciálható f(x) függvény, akkor ebben a pontban extrémum jelenik meg.

Elegendő állapot

1. Ha a derivált előjele pluszról mínuszra változik, akkor x_(0) lesz a minimumpont;
2. x_(0) - csak akkor lesz maximális pont, ha a derivált mínuszról pluszra változtatja az előjelet, amikor áthalad az x_(0) stacionárius ponton.

A függvény legnagyobb és legkisebb értéke az intervallumon

A számítás lépései:

1. Az f"(x) származékot keresem;
2. Megkeressük a függvény stacionárius és kritikus pontjait, és kiválasztjuk az intervallumhoz tartozókat;
3. Az f(x) függvény értékei a stacionárius ill kritikus pontokés a szegmens végeit. Az eredmények közül a legkisebb lesz a legkisebb érték funkciókat, és több - legnagyobb.

A páros és páratlan függvények grafikonjai a következő tulajdonságokkal rendelkeznek:

Ha egy függvény páros, akkor a grafikonja szimmetrikus az y tengelyre. Ha egy függvény páratlan, akkor a grafikonja szimmetrikus az origóra.

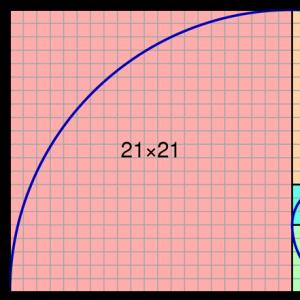
Példa.Ábrázolja a \(y=\left|x \right|\) függvényt.

Megoldás. Tekintsük a következő függvényt: \(f\left(x \right)=\left|x \right|\) és helyettesítsük \(x \)-vel az ellenkezőjét \(-x \). Egyszerű átalakítások eredményeként a következőt kapjuk: $$f\left(-x \right)=\left|-x \right|=\left|x \right|=f\left(x \right)$$ In Más szóval, ha az argumentumot ellentétes előjelre cseréljük, a függvény nem fog megváltozni.

Ez azt jelenti, hogy ez a függvény páros, és a grafikonja szimmetrikus lesz az y tengelyre (függőleges tengely). Ennek a függvénynek a grafikonja a bal oldali ábrán látható. Ez azt jelenti, hogy a grafikon ábrázolásakor csak a felét, a második részt rajzolhatja meg (a függőleges tengelytől balra, jobbra már szimmetrikusan rajzolja). Ha meghatározza egy függvény szimmetriáját, mielőtt elkezdi ábrázolni a grafikonját, nagyban leegyszerűsítheti a függvény összeállításának vagy tanulmányozásának folyamatát. Ha nehéz a bejelentkezés Általános nézet, akkor könnyebben megteheti: helyettesítse be ugyanazokat az értékeket különböző előjelekkel az egyenletbe. Például -5 és 5. Ha a függvény értékei megegyeznek, akkor remélhetjük, hogy a függvény páros lesz. Matematikai szempontból ez a megközelítés nem teljesen helyes, de gyakorlati szempontból kényelmes. Az eredmény megbízhatóságának növelése érdekében több ilyen ellentétes értékpárt helyettesíthet.

Példa.Ábrázolja a \(y=x\left|x \right|\) függvényt.

Megoldás. Ellenőrizzük ugyanazt, mint az előző példában: $$f\left(-x \right)=x\left|-x \right|=-x\left|x \right|=-f\left(x \right) ) $$ Ez azt jelenti, hogy az eredeti függvény páratlan (a függvény előjele megfordul).

Következtetés: a függvény szimmetrikus az origóhoz képest. Csak az egyik felét építheti meg, a másik felét pedig szimmetrikusan rajzolhatja meg. Ezt a szimmetriát nehezebb megrajzolni. Ez azt jelenti, hogy a diagramot a lap másik oldaláról nézi, és még fejjel lefelé is fordítja. És ezt is megteheti: vegye a megrajzolt részt és forgassa el az origó körül 180 fokkal az óramutató járásával ellentétes irányba.

Példa.Ábrázolja a \(y=x^3+x^2\) függvényt.

Megoldás. Végezzük el ugyanazt az előjelváltozás ellenőrzését, mint az előző két példában. $$f\left(-x \right)=\left(-x \right)^3+\left(-x \right)^2=-x^2+x^2$$ $$f\left( -x \right)\not=f\left(x \right),f\left(-x \right)\not=-f\left(x \right)$$ Ami azt jelenti, hogy a függvény nem páros és nem páratlan .

Következtetés: a függvény nem szimmetrikus sem a koordináta-rendszer origójára, sem középpontjára. Ez azért történt, mert ez két függvény összege: páros és páratlan. Ugyanez a helyzet lesz, ha kivonunk két különböző függvényt. De a szorzás vagy osztás más eredményhez vezet. Például egy páros és egy páratlan függvény szorzata páratlant ad. Vagy a két páratlan hányadosa páros függvényhez vezet.