Kúp metszete függőleges síkkal. Kúp metszetének szerkesztése síkkal

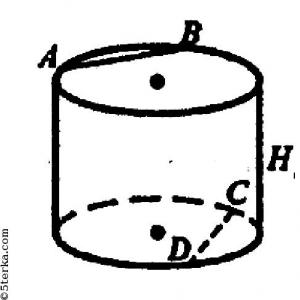
90°

2. Mekkora a hengernek a generatrixával párhuzamos sík metszete?

A szakasz egy téglalap.

3. A henger tövében két, egymással nem párhuzamos húrt veszünk. Lehet-e ezen húrok pontjai közötti legrövidebb távolság: a) egyenlő a henger magasságával; b) nagyobb, mint a henger magassága; c) kisebb, mint a henger magassága?

AB és CD párhuzamos síkban helyezkednek el.

H a henger magassága.

4. Két hengeres részt azonos vastagságú nikkelréteggel vonnak be. Az első rész magassága kétszerese a másodikénak, de alapjának sugara fele a második rész alapjának sugarának. Melyik rész használ több nikkelt?

Első rész Második rész

2l, l - magasság (generatív),

r/2, r - alapsugár,

Az oldalfelületek egyenlőek, de a második rész két alapterülete nagyobb, mint az első rész két alapjának területe.

5. Egyenlőek-e egymással a kúp generatricái és: a) az alap síkja közötti szögek? b) a tengelye?

a) igen; b) igen.

6. Mekkora a kúpnak a csúcsán áthaladó sík metszete?

Egyenlő szárú háromszög.

7. Az A és B pont a labdához tartozik. Ez a golyó az AB szakasz bármely pontjához tartozik?

8. Fekszik-e egy 4 cm és 2 √2 cm oldalú derékszögű háromszög összes csúcsa egy √5 cm sugarú gömbön?

Számítsuk ki egy derékszögű háromszög befogóját:

A hipotenusz nem fér el a gömbön belül, akkor legalább egy csúcs a gömbön kívül van.

9. Lehet-e két közös középpontú és nem egyenlő sugarú gömbnek közös érintősíkja?

Az egyik gömb mindig a másik belsejében lesz, ezért lehetetlen közös érintősíkot rajzolni.

10. Mennyi a tér azon pontjainak halmaza, amelyekből egy adott szakasz derékszögben látható?

Ez egy olyan gömb, amelynek ez a szegmens az átmérője.

Az iskolai geometriatanfolyam feladatainak megoldása során a kúp két síkbeli metszetét veszik figyelembe:

· a kúp tengelyére merőleges metszetek – körökben;

· a kúp tetején átmenő szakaszok – egyenlő szárú háromszögek;

A kúpnak a tengelyén átmenő sík metszetét ún axiális szakasz .

A kúpos felület síkszelvényeinek típusai:

·
a kúpos felület tengelyére merőleges metszet – kör ;

· az egyik generatricával párhuzamos szakasz – parabola azok. ______________________________________

· két generatricával párhuzamos szakasz – hiperbola, i.e. pontok halmaza egy síkon, a távolságok különbségének modulusa, amelytől a síkon két adott pontig tart, állandó érték.

· a kúpos felület tengelyére nem merőleges és nem párhuzamos metszet – ellipszis.

· két generatricán áthaladó szakasz – metsző vonalpár;

Bizonyítsunk be két állítást.

2. állítás. A kúp két generatricájával párhuzamos kúpos felület metszet hiperbola.

A kúp két generátorával párhuzamos α sík metszi a kúp felületét egy bizonyos egyenes mentén l. Bizonyítsuk be, hogy ez az egyenes hiperbola.

Vegyünk két egyforma golyót, amelyek érintik a kúp oldalfelületét és a metszetsíkot. Hagyja a pontokat F 1 és F 2 – érintkezési pontok a metszősíkkal. Egy tetszőleges ponton keresztül M vonalak l rajzoljunk generatrixot t. Legyen a szakasz hossza A.A. Ennek a generatrixnak az 1-je, a golyók átmérős síkjai közé zárva, merőleges a kúp generátoraira, egyenlő 2-vel a. Ezután az érintők tulajdonsága alapján M.F. 1 =M.A. 1 , M.F. 2 = M.A. 2 ezért | M.F. 1 –M.F. 2 |=|M.A. 1 –M.A. 2 =2a|, azaz | M.F. 1 –M.F. 2 | = const, ami a vonalat jelenti l– ellipszis.

3. állítás. A kúpos felület olyan szakasza, amely nem merőleges és nem párhuzamos a kúpos felület tengelyére - ellipszis.

Készíts egy rajzot, és bizonyítsd be magad.

2.4. csonka kúp

Csonkakúp a kúpnak azt a részét, amely az alapja és a kúp tengelyére merőleges vágósík között helyezkedik el. Ennek a kúpnak az alapját és a keresztmetszetben kapott kört ún okokból csonkakúp. Magasság a csonka kúp az alapjainak középpontját összekötő szakasz; oldalsó felület– egy csonkakúp alapjai között elhelyezkedő kúpos felület része. A csonka kúp alapjai között elhelyezkedő kúpos felület generatricáinak szegmenseit nevezzük alakítás.

Csonkakúpot úgy kaphatunk, hogy egy téglalap alakú trapézt az alapokra merőleges oldala köré forgatunk.

Tétel(egy csonka kúp oldalfelületén). A csonka kúp oldalfelületének területe megegyezik az alapok körei hosszának összegének felével és a generatrix hosszával: , Hol RÉs r- az alapok sugarai, l– a generatrix hossza.

Tétel(csonkakúp térfogatán). Egy csonka kúp térfogata, amelynek magassága a H, és az alapok sugara egyenlő RÉs r képlettel számolva
.

Gömb és labda

Tétel (egy gömb és egy sík egymáshoz viszonyított helyzetéről). Hadd d- távolság a központtól O gömb sugara r az α síkra. Majd:

1) ha d < r, akkor a gömb α sík szerinti metszete egy középpontú kör O 1 sugár , Hol O 1 – pontvetítés O az α síkra;

2) ha d = r, akkor a gömbnek és a síknak csak egy közös pontja van;

3) ha d > r, akkor a gömbnek és a síknak nincs közös pontja.

1) Hagyjuk d < r, az a sík metszi a gömböt W( O, r) valamilyen vonal mentén L. Legyen a lényeg M– az egyenes tetszőleges pontja L, majd a háromszögben O.O. 1 M:

Ð O.O. 1 M=90° ( O.O. 1 ^M.O. 1, mert O.O. 1 ^a és M.O. 1 Ìa), láb M.O. 1 = . Ez azt jelenti, hogy a vonal minden pontja L egyenlő távolságra a ponttól O 1, ezért a gömb a sík szerinti metszete egy kör, amelynek középpontja a pontban van O 1 és sugár .

2) Hagyjuk d = r. Távolság a ponttól O az a síkhoz kisebb, mint a pont távolsága O O 1 pontot jelent O Az 1 az a sík egyetlen pontja, amely a gömbhöz tartozik.

3) Hagyjuk d > r. Távolság a ponttól O az a sík bármely pontjához, amely különbözik a ponttól O 1, több d. A d > r, ami azt jelenti, hogy a gömbnek és a síknak nincs közös pontja.

Következmény. A gömbnek egy sík szerinti metszete egy kör.

A gömb (gömb) középpontján áthaladó síkot ún középsík, és ennek a síknak a szakasza a nagy kör (nagy kör). A középsíkra merőleges átmérő végeit ún a gömb pólusai.

Egy gömb (golyó) érintősíkja A síkot olyan síknak nevezzük, amelynek csak egy közös pontja van egy gömbbel (golyóval). Úgy hívják érintkezési pont. Egy gömb (golyó) érintősíkjában fekvő és az érintkezési ponton átmenő egyenest ún. érintővonal a gömbhöz (labdához).

Tétel(érintő sík jel)

Tétel(az érintősík tulajdonságáról)

Gömb alakú (golyós) szegmens a gömb (golyó) sík által levágott részét nevezzük. Azt a kört (kört), amely mentén a sík a gömböt (golyót) metszi, ún gömb alakú (golyós) szegmensek alapja, amelyre a sík felosztja a gömböt. Gömb alakú (golyó) magassága szegmens az alap és a gömb között elhelyezkedő szakasz alapjára merőleges átmérőjű szakasz hossza. (A képen A.F.És B.F.– a megfelelő gömb (golyó) szegmensek magassága).

Gömb alakú öv (gömb alakú réteg ) a gömb (golyó) két párhuzamos vágási sík között elhelyezkedő része. A gömböv alapjai (gömbréteg) köröknek (köröknek) nevezzük, amelyeket egy gömb (golyó) metszetében ezek a síkok kapnak. A gömböv magassága (gömb alakú réteg) síkok közötti távolságnak nevezzük. (A képen F.E.– a gömböv (gömb alakú réteg) magassága.)

Labda szektor egy geometriai test, amelyet egy 90°-nál kisebb szögű körszektornak a körszektort korlátozó sugarak egyikét tartalmazó egyenes körüli elforgatásával nyernek. A gömb alakú szektor egy gömb alakú szegmensből és egy kúpból áll. A labdaszektor magassága a megfelelő gömbszakasz magasságát ún. (A képen AB– a gömb alakú szektor magassága).

Egy gömb alakú szegmens területe , Hol R- a gömb sugara, h– szegmens magasság.

A gömböv területe , Hol R- a gömb sugara, h- derékmagasság.

Egy gömb területe , Hol R– a gömb sugara.

A gömbi szektor térfogata , Hol R- a labda sugara, h– szektor magassága.

Golyószegmens térfogata
, Hol R- a labda sugara, h– szegmens magasság.

Gömb térfogata , Hol R– a labda sugara.

Ha egy jobb oldali körkúp metszi a síkot, a következő másodrendű görbék képezhetők: kör, ellipszis, hiperbola és parabola. Ezen görbék megjelenése a vágási sík kúpos felület tengelyéhez viszonyított dőlésszögétől függ.

Az alábbiakban megvizsgálunk egy olyan problémát, amelyben egy ω kúp α síkbeli metszetének vetületeit és természetes méretét kell megszerkeszteni. A kiinduló adatokat az alábbi ábra mutatja be.

A szakasz legmagasabb és legalacsonyabb pontjainak meghatározása. Láthatósági korlátok

A metszésvonal megépítését a jellegzetes pontjainak megtalálásával kell kezdeni. Meghatározzák a szakasz határait és láthatóságát a megfigyelőhöz képest.

A kúpos felület tengelyén keresztül P 2 -vel párhuzamos γ segédsíkot rajzolunk. Két generátor mentén metszi az ω kúpot, az f γ frontális mentén pedig az α síkot. Az f γ és a generátorok metszéspontjának 1. és 2. pontja határpontok. Felosztják a szakaszt látható és láthatatlan részekre.

Határozzuk meg a metszésvonal legmagasabb és legalacsonyabb pontját. Ehhez a kúptengelyen át vezetünk be egy további β vágósíkot h 0 α-ra merőlegesen. Az SL és SK generátorok mentén metszi a kúpos felületet, az MN egyenes mentén pedig az α síkot. A szükséges 3 = SL ∩ MN és 4 = SK ∩ MN pontok határozzák meg az ellipszis főtengelyét. Középpontja az O pontban van, amely kettévágja a 3-4 szakaszt.

Közbenső pontok meghatározása és ellipszis vetületek felépítése

A metszetkivetítések legpontosabb megszerkesztéséhez számos további pontot találunk. Ellipszis esetén annak kis átmérőjének értékét célszerű meghatározni. Ehhez rajzoljon egy δ segédvízszintes síkot az O középponton keresztül. A kúpos felületet AB átmérőjű kör mentén metszi, az α sík pedig vízszintesen h δ. Megszerkesztjük a kör és a h δ egyenes vízszintes vetületeit. Ezek metszéspontja határozza meg az ellipszis kis átmérőjének 5" és 6" pontját.

A 7. és 8. közbenső pont megalkotásához bevezetünk egy ε vízszintes segédsíkot. A 7" és 8" kiemelkedés az 5" és 6"-hoz hasonlóan van meghatározva, amint az az ábrán látható.

A talált pontokat sima görbével összekötve egy elliptikus metszet kontúrját kaptuk. Az ábrán pirossal van jelölve. A kontúr elülső vetülete megváltoztatja láthatóságát az 1. és 2. pontban, amint azt fentebb megjegyeztük.

A metszet természetes méretének meghatározásához az α síkot addig forgatjuk, amíg az egy vonalba nem kerül a vízszintes síkkal. A h 0 α nyomvonalat fogjuk használni forgástengelyként. Helye az átalakulási folyamatban változatlan marad.

A konstrukció a frontális f 1 α irányának meghatározásával kezdődik. Az f 0 α egyenesre felveszünk egy tetszőleges E pontot és meghatározzuk ennek E vetületét. E-ből merőlegest ejtünk h 0 α-ra. Ennek a merőlegesnek az X α E"" sugarú körrel való metszéspontja határozza meg az E" 1 pont helyzetét. X α és E" 1 pontokon keresztül f 1 α-t rajzolunk.

Megszerkesztjük a h" 1 δ ∥ h 0 α vízszintes egyenes vetületét, amint az az ábrán látható. Az O" 1 és 5" 1, 6" 1 pontok h" 1 δ metszéspontjában helyezkednek el h-ra merőleges vonalakkal. 0 α az O"-ból és 5", 6". Hasonlóképpen a vízszintes h" 1 ε-n 7" 1 és 8" 1 található.

Megszerkesztjük az f" 1 γ ∥ f 1 α, f" 3 ∥ f 1 α és f" 4 ∥ f 1 α frontális vetületeit. Az 1" 1, 2" 1, 3" 1 és 4" 1 pontok a metszéspontban vannak ezek közül az elülső oldalak merőlegesei h 0α-ra visszaállítva 1", 2", 3" és 4"-ről.

Kúp. A kúp tengelyirányú szakasza. Kúp metszete síkok szerint. Csonkakúp. Felírt és körülírt piramisok és kúpok

Kúp- ez egy test, amely egy körből áll, egy pontból, amely nem a kör síkján fekszik, és szakaszokból, amelyek összekötik ezt a pontot a kör pontjaival.

A kúp alapja egy kör, a kúp csúcsa egy olyan pont, amely nem esik a kör területén, a kúp alkotó részei a kúp csúcsát a kör pontjaival összekötő szakaszok. az alap köre.

Egy kúp akkor egyenes, ha a kúp tetejét az alapja középpontjával összekötő egyenes merőleges az alap síkjára. A kúp magassága a felülről az alap területére húzott merőleges.

A jobb oldali kúp tengelye egy egyenes, amely tartalmazza a magasságát.

Egy egyenes kúp alapjával párhuzamos sík körben metszi a kúpot, az oldalfelületet pedig körben a kúp tengelyén lévő középponttal.

Ha a vágási sík átmegy a kúp tengelyén, akkor a metszetét egy egyenlő szárú háromszög, melynek alapja egyenlő a kúp alapjának átmérőjével, oldalai pedig a kúp generátorai. Ezt a szakaszt axiálisnak nevezzük.

Egy kúp, amelynek tengelyirányú keresztmetszete egyenlő oldalú háromszög, egyenlő oldalú kúpnak nevezzük. Ha a vágósík a kúp csúcsán az alap síkjával szöget zár be, akkor a metszete egy egyenlő szárú háromszög, melynek alapja a kúp alapjának húrja, az oldalai pedig a kúp generátorai. a kúp.

Ha a vágási sík párhuzamosan fut a kúp alapjával, akkor a metszet egy kör, amelynek középpontja a kúp tengelye. Egy ilyen vágósík a kúpot két részre vágja - egy kúpra és egy csonka kúpra. Ennek a kúpnak a párhuzamos síkjaiban fekvő körök az alapjai; a középpontjukat összekötő szakasz a csonkakúp magassága.

Kúpba írt piramis, olyan piramisnak nevezzük, amelynek alapja a kúp alapjának körébe írt sokszög, a teteje pedig a kúp teteje. A kúpba írt gúla oldalsó élei alkotják a kúpot.

Érintősík a kúphoz a kúp generatrixán átmenő és ezt a generatrixot tartalmazó tengelymetszet síkjára merőleges síknak nevezzük.

A kúp körül körülírt gúla az a gúla, amelynek alapja a kúp alapja körül körülírt sokszög, és a csúcsa egybeesik a kúp csúcsával.

A leírt gúla oldallapjainak síkjai a kúp érintősíkai.

Ez érdekes. Ha a geometriában az alakok ábrázolására párhuzamos vetítést alkalmaznak, akkor a festészetben, az építészetben és a fényképezésben központi vetítést alkalmaznak.

Például egy bizonyos O pont (a tervezési középpont) és egy α sík, amely nem megy át ezen a ponton, rögzített a térben. A tér egy pontján és a tervezési középponton keresztül egy egyenes vonalat húzunk, amely egy adott síkot egy pontban metszi, amelyet a pont síkra vetített központi vetületének nevezünk. A központi kialakítás nem őrzi meg a párhuzamosságot. A térbeli alakzatok síkon való ábrázolását központi vetítéssel perspektívának nevezzük. Leonardo da Vinci és Albrecht Durer művészek a perspektíva elméletét tanulmányozták.

Amelyek egy pontból (a kúp tetejéről) erednek, és amelyek sík felületen mennek keresztül.

Előfordul, hogy a kúp a test egy korlátozott térfogatú része, és egy sík felület csúcsát és pontjait összekötő egyes szegmensek kombinálásával keletkezik. Jelen esetben ez utóbbi a kúp alapja, és a kúp állítólag ezen az alapon nyugszik.

Ha egy kúp alapja sokszög, az már az piramis .

Kör alakú kúp- ez egy test, amely egy körből (a kúp alapjából) áll, egy pontból, amely nem e kör síkjában fekszik (a kúp teteje és minden olyan szegmens, amely a kúp tetejét összeköti a kör pontjaival bázis).

A kúp csúcsát és az alapkör pontjait összekötő szakaszokat nevezzük kúpot képezve. A kúp felülete egy alapból és egy oldalfelületből áll.

Az oldalsó felület megfelelő n- egy kúpba írt szénpiramis:

S n =½P n l n,

Ahol Pn- a piramis alapjának kerülete, és l n- apotém.

Ugyanezen elv szerint: egy alapsugárral rendelkező csonka kúp oldalfelületére R 1, R 2és formálása l a következő képletet kapjuk:

S=(R1+R2)l.

Egyenes és ferde körkúpok azonos alappal és magassággal. Ezeknek a testeknek a térfogata azonos:

A kúp tulajdonságai.

Ha az alapterületnek van határa, ez azt jelenti, hogy a kúp térfogatának is van határa, és egyenlő az alap magasságának és területének szorzatának harmadik részével.

Ahol S- alapterület, H- magasság.

Így minden kúp, amely ezen az alapon nyugszik, és amelynek csúcsa az alappal párhuzamos síkon helyezkedik el, azonos térfogatú, mivel magasságuk azonos.

A határértékkel rendelkező kúpok súlypontja az alaptól számított magasság negyedében található.
A derékszögű körkúp csúcsánál lévő térszög a következő képlettel fejezhető ki: