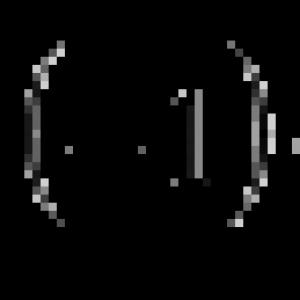Geometriai figurák. Piramis

• apotém- egy szabályos gúla oldallapjának magassága, amelyet a csúcsából húzunk (ráadásul az apotém a merőleges hossza, amely a szabályos sokszög közepétől az egyik oldalára süllyeszthető);
• oldalsó arcok (ASB, BSC, CSD, DSA) - háromszögek, amelyek a csúcsban találkoznak;
• oldalsó bordák ( MINT , B.S. , C.S. , D.S. ) — az oldallapok közös oldalai;
• a piramis teteje (t. S) - az oldalbordákat összekötő pont, amely nem az alap síkjában fekszik;
• magasság ( ÍGY ) - a piramis tetején keresztül az alap síkjához húzott merőleges szakasz (egy ilyen szakasz vége a gúla teteje és a merőleges alapja lesz);
• a piramis átlós metszete- a piramis egy szakasza, amely áthalad a tetején és az alap átlóján;
• bázis (ABCD) - sokszög, amely nem tartozik a piramis csúcsához.

A piramis tulajdonságai.

1. Ha minden oldalsó él azonos méretű, akkor:

• könnyű leírni egy kört a piramis alapjához közel, és a piramis teteje ennek a körnek a közepébe lesz vetítve;
• az oldalbordák az alap síkjával egyenlő szöget zárnak be;
• Ráadásul ennek az ellenkezője is igaz, pl. ha az oldalbordák egyenlő szöget zárnak be az alap síkjával, vagy ha egy kör írható le a piramis alapja körül, és a gúla teteje ennek a körnek a közepébe lesz vetítve, ez azt jelenti, hogy az összes oldalél a piramis azonos méretűek.

2. Ha az oldallapok dőlésszöge az alap síkjához képest azonos értékű, akkor:

• könnyű leírni egy kört a piramis alapjához közel, és a piramis teteje ennek a körnek a közepébe lesz vetítve;
• az oldallapok magassága egyenlő hosszúságú;
• az oldalfelület területe egyenlő az alap kerületének és az oldalfelület magasságának szorzatával.

3. A gúla körül gömb írható le, ha a gúla alján van egy sokszög, amely körül kör írható le (szükséges és elégséges feltétel). A gömb középpontja azoknak a síkoknak a metszéspontja lesz, amelyek átmennek a piramis rájuk merőleges éleinek közepén. Ebből a tételből arra a következtetésre jutunk, hogy egy gömb leírható bármely háromszög és bármely szabályos piramis körül.

4. Gúlába akkor írhatunk be gömböt, ha a gúla belső diéderszögeinek felezősíkjai az 1. pontban metszik egymást (szükséges és elégséges feltétel). Ez a pont lesz a gömb középpontja.

A legegyszerűbb piramis.

A szögek száma alapján a piramis alapja háromszögre, négyszögre stb.

Piramis lesz háromszög alakú, négyszögű, és így tovább, amikor a piramis alapja egy háromszög, egy négyszög stb. A háromszög alakú piramis egy tetraéder - egy tetraéder. Négyszögletű - ötszögletű és így tovább.

Itt alapvető információkat talál a piramisokról és a kapcsolódó képletekről és fogalmakról. Mindegyiket matematika oktatóval tanulják az egységes államvizsgára készülve.

Vegyünk egy síkot, egy sokszöget , benne fekve és egy S ponttal, nem benne fekve. Kössük össze S-t a sokszög összes csúcsával. A kapott poliédert piramisnak nevezzük. A szegmenseket oldalbordáknak nevezzük. A sokszöget alapnak nevezzük, az S pontot pedig a piramis csúcsa. Az n számtól függően a piramist háromszögnek (n=3), négyszögletűnek (n=4), ötszögletűnek (n=5) és így tovább nevezzük. A háromszög alakú piramis alternatív neve tetraéder. A piramis magassága az a merőleges, amely a tetejétől az alap síkjához ereszkedik.

A piramist szabályosnak nevezzük, ha szabályos sokszög, és a piramis magasságának alapja (a merőleges alapja) a középpontja.

Az oktató megjegyzése:
Ne keverje össze a „szabályos piramis” és a „szabályos tetraéder” fogalmát. Egy szabályos piramisban az oldalélek nem feltétlenül egyenlőek az alap éleivel, de egy szabályos tetraéderben mind a 6 él egyenlő. Ez az ő meghatározása. Könnyű bizonyítani, hogy az egyenlőségből következik, hogy a sokszög P középpontja egybeesik alapmagassággal, tehát a szabályos tetraéder szabályos gúla.

Mi az apotém?
A piramis apotémája az oldallap magassága. Ha a piramis szabályos, akkor minden apotémája egyenlő. Ennek a fordítottja nem igaz.

Egy matematika tanár a terminológiájáról: a piramisokkal végzett munka 80%-a kétféle háromszögből épül fel:
1) Apothem SK és magasság SP
2) Tartalmazza az SA oldalélt és annak PA vetületét

Az ezekre a háromszögekre való hivatkozások egyszerűsítése érdekében kényelmesebb, ha a matektanár az elsőt hívja meg. apothematikus, és a második tengerparti. Sajnos ezt a terminológiát egyik tankönyvben sem találja meg, a tanárnak kell egyoldalúan bevezetnie.

A piramis térfogatának képlete:
1) , ahol a piramis alapterülete és a piramis magassága
2) , ahol a beírt gömb sugara, és a piramis teljes felületének területe.
3) , ahol MN bármely két keresztező él közötti távolság, és a négy fennmaradó él felezőpontjai által alkotott paralelogramma területe.

A piramis magasságának alapja:

A P pont (lásd az ábrát) egybeesik a piramis alján lévő beírt kör középpontjával, ha az alábbi feltételek egyike teljesül:
1) Minden apotém egyenlő
2) Minden oldalfelület egyformán dől az alaphoz
3) Minden apotém egyformán hajlik a piramis magasságára
4) A piramis magassága egyformán ferde minden oldallaphoz

A matektanár megjegyzése: Kérjük, vegye figyelembe, hogy minden pontot egy közös tulajdonság egyesít: így vagy úgy, az oldallapok mindenhol érintettek (az apotémek az elemeik). Ezért az oktató egy kevésbé pontos, de a tanuláshoz kényelmesebb megfogalmazást tud ajánlani: a P pont egybeesik a beírt kör középpontjával, a gúla alapjával, ha ennek oldallapjairól azonos információ áll rendelkezésre. Ennek bizonyításához elég megmutatni, hogy minden apotém háromszög egyenlő.

A P pont egybeesik a piramis alapja közelében körülírt kör középpontjával, ha a három feltétel egyike teljesül:
1) Minden oldalél egyenlő
2) Minden oldalborda egyformán dől az alaphoz
3) Minden oldalborda egyformán dől a magassághoz

1. fejezet A metszettípusok elméleti tanulmányozása és építési módszerek szabályos négyszög alakú piramisban

A piramis (ógörögül Πυραμίς, P. πυραμίδος) egy poliéder, amelynek alapja egy sokszög, a fennmaradó lapok pedig közös csúcsú háromszögek. Az alapszögek száma alapján a piramisokat három-, négyszögletűnek stb. különböztetjük meg. A gúla a kúp speciális esete.

A piramisgeometria az ókori Egyiptomban és Babilonban kezdődött, de az ókori Görögországban aktívan fejlesztették. A piramis térfogatát először Démokritosz állapította meg, és ezt Cnidus Eudoxus is bebizonyította. Az ókori görög matematikus, Eukleidész „Elemek” című könyvének XII. kötetében rendszerezte a piramisról szóló ismereteket, és levezette a piramis első meghatározását is: fizikai alak, amelyet egy síkból egy pontba konvergáló síkok határolnak.

Piramis elemek

· apotém - egy szabályos piramis oldallapjának magassága, a tetejétől húzva;

· oldallapok - a piramis tetején összefutó háromszögek;

· oldalbordák – az oldallapok közös oldalai;

· a gúla csúcsa az oldalbordákat összekötő pont, amely nem esik az alap síkjában;

· magasság - a piramis tetején keresztül az alap síkjához húzott merőleges szakasz (ennek a szakasznak a vége a piramis teteje és a merőleges alapja);

· piramis átlós metszete - a piramis egy szakasza, amely áthalad az alap tetején és átlójában;

· alap - sokszög, amely nem tartozik a piramis tetejéhez.

A piramis tulajdonságai:

A piramis lapjainak száma megegyezik a csúcsok számával.

Minden olyan poliéder, amelynek lapjainak száma megegyezik a csúcsok számával, piramis. A piramis csúcsainak teljes száma n+1, ahol n az alján lévő csúcsok száma.

Ha minden oldalél egyenlő, Ez:

§ egy kör írható le a piramis alapja közelében, amelynek a gúla teteje a középpontjába vetül;

§ Az oldalbordák az alap síkjával egyenlő szöget zárnak be.

§ fordítva is igaz, vagyis ha az oldalélek egyenlő szöget zárnak be az alap síkjával, vagy ha a gúla alapja körül kör írható le, amelynek a gúla teteje a középpontjába vetül, akkor a piramis minden oldaléle egyenlő.

Ha az oldallapok ugyanabban a szögben dőlnek az alapsíkhoz, Ez:

§ a piramis aljába kör írható, amelynek középpontjába a gúla teteje vetíthető;

§ az oldallapok magassága egyenlő;

§ Az oldalfelület területe egyenlő az alap kerülete és az oldalfelület magasságának szorzatának felével.

A szabályos négyszög alakú piramis metszeteinek típusai:

· a piramis átlós metszete;

Ez a lecke egy szabályos háromszög alakú piramis és speciális esete, a tetraéder definícióját és tulajdonságait ismerteti (lásd alább). A lecke végén hivatkozások találhatók a problémamegoldási példákra.

Meghatározás

Szabályos háromszög alakú piramis egy piramis, amelynek alapja egy szabályos háromszög, és a csúcsa az alap közepébe van vetítve.

Az ábrán látható:
ABC- Bázis piramisok
OS - Magasság
KS – Apothem
OK - az alapra írt kör sugara
AO - egy szabályos háromszög alakú piramis alapja körül körülírt kör sugara
SKO - diéder szög a piramis alapja és lapja között (egy szabályos piramisban egyenlők)

Fontos. Egy szabályos háromszög alakú gúlában az él hossza (az ábrán AS, BS, CS) nem feltétlenül egyezik meg az alapoldal hosszával (AB, AC, BC az ábrán). Ha egy szabályos háromszög alakú gúla élének hossza megegyezik az alap oldalának hosszával, akkor az ilyen piramist tetraédernek nevezzük (lásd alább).

Szabályos háromszög alakú piramis tulajdonságai:

• szabályos gúla oldalélei egyenlők
• egy szabályos gúla minden oldallapja egyenlő szárú háromszög
• egy szabályos háromszög alakú piramisban vagy elhelyezhet egy gömböt, vagy körülírhatja
• ha egy szabályos háromszög alakú gúla köré írt és körülírt gömb középpontjai egybeesnek, akkor a gúla tetején lévő síkszögek összege π (180 fok), és mindegyik egyenlő π / 3 ( pi osztva 3 vagy 60 fokkal).
• Egy szabályos gúla oldalfelületének területe egyenlő az alap kerülete és az apotém szorzatának felével
• a piramis csúcsát az alapra vetítjük egy szabályos egyenlő oldalú háromszög középpontjába, amely a beírt kör középpontja és a mediánok metszéspontja

Képletek egy szabályos háromszög alakú piramishoz

A szabályos háromszög alakú piramis térfogatának képlete:

V egy szabályos gúla térfogata, amelynek alapjában szabályos (egyenlő oldalú) háromszög található
h - a piramis magassága
a a gúla alapja oldalának hossza
R - körsugár
r - a beírt kör sugara

Mivel a szabályos háromszög alakú gúla a szabályos piramis speciális esete, a szabályos gúlára érvényes képletek a szabályos háromszög alakúra is igazak - ld. szabályos piramis képletei.

Példák problémamegoldásra:

Tetraéder

A szabályos háromszög alakú piramis speciális esete az tetraéder.

Tetraéder- ez egy szabályos poliéder (szabályos háromszög alakú piramis), amelyben minden lap szabályos háromszög.

Tetraéderhez:

• Minden él egyenlő
• 4 lap, 4 csúcs és 6 él
• Minden éleknél lévő kétszög és a csúcsokban lévő háromszög egyenlő

Tetraéder mediánja- ez egy szegmens, amely egy csúcsot köt össze a szemközti lap mediánjainak metszéspontjával (a csúcstal szemközti egyenlő oldalú háromszög mediánjai)

Tetraéder bimediánja- ez egy szakasz, amely összeköti a keresztező élek felezőpontjait (egy háromszög oldalainak felezőpontjait köti össze, amely a tetraéder egyik lapja)

A tetraéder magassága- ez egy szegmens, amely egy csúcsot összeköt a szemközti lapon lévő ponttal, és merőleges erre a lapra (azaz bármely lapból húzott magasság, amely egybeesik a körülírt kör középpontjával is).

Tetraéder a következőkkel rendelkezik tulajdonságait:

• A tetraéder minden mediánja és bimediánja egy pontban metszi egymást
• Ez a pont a csúcstól számítva 3:1 arányban osztja el a mediánokat
• Ez a pont kettéosztja a bimediánokat