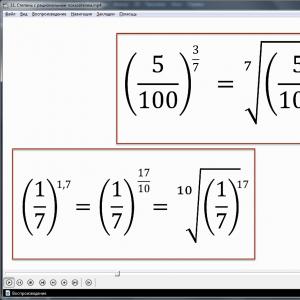
Классическая вероятность. Вероятность случайного события
как онтологическая категория отражает меру возможности возникновения какого-либо сущего в каких-либо условиях. В отличие от математических и логической интерпретации этого понятия онтологическая В. не связывает себя с обязательностью количетвенного выражения. Значение В. раскрывается в контексте понимания детерминизма и характера развития в целом.
Отличное определение
Неполное определение ↓
ВЕРОЯТНОСТЬ
понятие, характеризующее количеств. меру возможности появления нек-рого события при определ. условиях. В науч. познании встречаются три интерпретации В. Классическая концепция В., возникшая из математич. анализа азартных игр и наиболее полно разработанная Б. Паскалем, Я. Бернулли и П. Лапласом, рассматривает В. как отношение числа благоприятствующих случаев к общему числу всех равновозможных. Напр., ири бросании игральной кости, имеющей 6 граней, выпадение каждой из них можно ожидать с В., равной 1/6, т. к. ни одна грань не имеет преимуществ перед другой. Подобная симметричность исходов опыта специально учитывается при организации игр, но сравнительно редко встречается при исследовании объективных событий в науке и практике. Классич. интерпретация В. уступила место статистич. концепции В., в основе к-рой лежат действит. наблюдения появления нек-рого события в ходе длит. опыта при точно фиксированных условиях. Практика подтверждает, что чем чаще происходит событие, тем больше степень объективной возможности его появления, или В. Поэтому статистич. интерпретация В. опирается на понятие относит. частоты, к-рое может быть определено опытным путем. В. как теоретич. понятие никогда не совпадает с эмпирически определяемой частотой, однако во мн. случаях она практически мало отличается от относит. частоты, найденной в результате длит. наблюдений. Многие статистики рассматривают В. как «двойник» относит. частоты, к-рая определяется при статистич. исследовании результатов наблюдений
или экспериментов. Менее реалистичным оказалось определение В. как предела относит. частот массовых событий, или коллективов, предложенное Р. Мизесом. В качестве дальнейшего развития частотного подхода к В. выдвигается диспозиционная, или пропенситивная, интерпретация В. (К. Поппер, Я. Хэккинг, М. Бунге, Т. Сетл). Согласно этой интерпретации, В. характеризует свойство порождающих условий, напр. эксперимент. установки, для получения последовательности массовых случайных событий. Именно такая установка порождает физич. диспозиции, или предрасположенности, В. к-рых может быть проверена с помощью относит. частот.
Статистич. интерпретация В. доминирует в науч. познании, ибо она отражает специфич. характер закономерностей, присущих массовым явлениям случайного характера. Во многих физич., биологич., экономич., демографич. и др. социальных процессах приходится учитывать действие множества случайных факторов, к-рые характеризуются устойчивой частотой. Выявление этой устойчивой частоты и количеств. ее оценка с помощью В. дает возможность вскрыть необходимость, к-рая прокладывает себе путь через совокупное действие множества случайностей. В этом находит свое проявление диалектика превращения случайности в необходимость (см. Ф. Энгельс, в кн.: Маркс К. и Энгельс Ф., Соч., т. 20, с. 535-36).
Логическая, или индуктивная, В. характеризует отношение между посылками и заключением недемонстративного и, в частности, индуктивного рассуждения. В отличие от дедукции, посылки индукции не гарантируют истинности заключения, а лишь делают его в той или иной степени правдоподобным. Это правдоподобие при точно сформулированных посылках иногда можно оценивать с помощью В. Значение этой В. чаще всего определяется посредством сравнит. понятий (больше, меньше или равно), а иногда и численным способом. Логич. интерпретацию часто используют для анализа индуктивных рассуждений и построения различных систем вероятностных логик (Р. Карнап, Р. Джефри). В семантич. концепции логич. В. часто определяется как степень подтверждения одного высказывания другими (напр., гипотезы ее эмпирич. данными) .
В связи с развитием теорий принятия решений и игр все большее распростраиение получает т. н. персоналистская интерпретация В. Хотя В. при этом выражает степень веры субъекта и появление нек-рого события, сами В. должны выбираться с таким расчетом, чтобы удовлетворялись аксиомы исчисления В. Поэтому В. при такой интерпретации выражает не столько степень субъективной, сколько разумной веры. Следовательно, решения, принимаемые на основе такой В., будут рациональными, ибо они не учитывают психологич. особенностей и склонностей субъекта.
С гносеологич. т. зр. различие между статистич., логич. и персоналистской интерпретациями В. состоит в том, что если первая дает характеристику объективным свойствам и отношениям массовых явлений случайного характера, то последние две анализируют особенности субъективной, познават. деятельности людей в условиях неопределенности.
ВЕРОЯТНОСТЬ
одно из важнейших понятий науки, характеризующее особое системное видение мира, его строения, эволюции и познания. Специфика вероятностного взгляда на мир раскрывается через включение в число базовых понятий бытия понятий случайности, независимости и иерархии (идеи уровней в структуре и детерминации систем).
Представления о вероятности зародились еще в древности и относились к характеристике нашего знания, при этом признавалось наличие вероятностного знания, отличающегося от достоверного знания и от ложного. Воздействие идеи вероятности на научное мышление, на развитие познания прямо связано с разработкой теории вероятностей как математической дисциплины. Зарождение математического учения о вероятности относится к 17 в., когда было положено начало разработке ядра понятий, допускающих. количественную (числовую) характеристику и выражающих вероятностную идею.
Интенсивные приложения вероятности к развитию познания приходятся на 2-ю пол. 19- 1-ю пол. 20 в. Вероятность вошла в структуры таких фундаментальных наук о природе, как классическая статистическая физика, генетика, квантовая теория, кибернетика (теория информации). Соответственно вероятность олицетворяет тот этап в развитии науки, который ныне определяется как неклассическая наука. Чтобы раскрыть новизну, особенности вероятностного образа мышления, необходимо исходить из анализа предмета теории вероятностей и оснований ее многочисленных приложений. Теорию вероятностей обычно определяют как математическую дисциплину, изучающую закономерности массовых случайных явлений при определенных условиях. Случайность означает, что в рамках массовости бытие каждого элементарного явления не зависит и не определяется бытием других явлений. В то же время сама массовость явлений обладает устойчивой структурой, содержит определенные регулярности. Массовое явление вполне строго делится на подсистемы, и относительное число элементарных явлений в каждой из подсистем (относительная частота) весьма устойчиво. Эта устойчивость сопоставляется с вероятностью. Массовое явление в целом характеризуется распределением вероятностей, т. е. заданием подсистем и соответствующих им вероятностей. Язык теории вероятностей есть язык вероятностных распределений. Соответственно теорию вероятностей и определяют как абстрактную науку об оперировании распределениями.
Вероятность породила в науке представления о статистических закономерностях и статистических системах. Последние суть системы, образованные из независимых или квазинезависимых сущностей, их структура характеризуется распределениями вероятностей. Но как возможно образование систем из независимых сущностей? Обычно предполагается, что для образования систем, имеющих целостные характеристики, необходимо, чтобы между их элементами существовали достаточно устойчивые связи, которые цементируют системы. Устойчивость статистическим системам придает наличие внешних условий, внешнего окружения, внешних, а не внутренних сил. Само определение вероятности всегда опирается на задание условий образования исходного массового явления. Еще одной важнейшей идеей, характеризующей вероятностную парадигму, является идея иерархии (субординации). Эта идея выражает взаимоотношения между характеристиками отдельных элементов и целостными характеристиками систем: последние как бы надстраиваются над первыми.
Значение вероятностных методов в познании заключается в том, что они позволяют исследовать и теоретически выражать закономерности строения и поведения объектов и систем, имеющих иерархическую, «двухуровневую» структуру.
Анализ природы вероятности опирается на частотную, статистическую ее трактовку. Вместе с тем весьма длительное время в науке господствовало такое понимание вероятности, которое получило название логической, или индуктивной, вероятности. Логическую вероятность интересуют вопросы обоснованности отдельного, индивидуального суждения в определенных условиях. Можно ли оценить степень подтверждения (достоверности, истинности) индуктивного заключения (гипотетического вывода) в количественной форме? В ходе становления теории вероятностей такие вопросы неоднократно обсуждались, и стали говорить о степенях подтверждения гипотетических заключений. Эта мера вероятности определяется имеющейся в распоряжении данного человека информацией, его опытом, воззрениями на мир и психологическим складом ума. Во всех подобных случаях величина вероятности не поддается строгим измерениям и практически лежит вне компетенции теории вероятностей как последовательной математической дисциплины.
Объективная, частотная трактовка вероятности утверждалась в науке со значительными трудностями. Первоначально на понимание природы вероятности оказали сильное воздействие те философско-методологические взгляды, которые были характерны для классической науки. Исторически становление вероятностных методов в физике происходило под определяющим воздействием идей механики: статистические системы трактовались просто как механические. Поскольку соответствующие задачи не решались строгими методами механики, то возникли утверждения, что обращение к вероятностным методам и статистическим закономерностям есть результат неполноты наших знаний. В истории развития классической статистической физики предпринимались многочисленные попытки обосновать ее на основе классической механики, однако все они потерпели неудачу. Основания вероятности состоят в том, что она выражает собою особенности структуры определенного класса систем, иного, чем системы механики: состояние элементов этих систем характеризуется неустойчивостью и особым (не сводящимся к механике) характером взаимодействий.
Вхождение вероятности в познание ведет к отрицанию концепции жесткого детерминизма, к отрицанию базовой модели бытия и познания, выработанных в процессе становления классической науки. Базовые модели, представленные статистическими теориями, носят иной, более общий характер: они включают в себя идеи случайности и независимости. Идея вероятности связана с раскрытием внутренней динамики объектов и систем, которая не может быть всецело определена внешними условиями и обстоятельствами.
Концепция вероятностного видения мира, опирающаяся на абсолютизацию представлений о независимости (как и прежде парадигма жесткой детерминации), в настоящее время выявила свою ограниченность, что наиболее сильно сказывается при переходе современной науки к аналитическим методам исследования сложноорганизованных систем и физико-математических основ явлений самоорганизации.
Отличное определение
Неполное определение ↓
«Читатель уже заметил в нашем изложении частое употребление понятия «вероятность».
Это характерная черта современной логики в противовес античной и средневековой логике. Современный логик понимает, что всё наше знание только в большей или меньшей степени вероятностно, а не достоверно, как привыкли думать философы и теологи. Он не слишком беспокоится из-за того, что индуктивный вывод придаёт лишь вероятность его заключению, поскольку он не ожидает ничего большего. Однако он задумается, если обнаружит причину сомневаться даже в вероятности своего заключения.
Таким образом, две проблемы получили в современной логике гораздо большую важность, чем в прежние времена. Во-первых, это природа вероятности, а во-вторых, значимость индукции. Обсудим вкратце эти проблемы.
Существует, соответственно, два вида вероятности - определённая и неопределённая.
Вероятность определённого вида имеет место в математической теории вероятности, где обсуждаются задачи типа метания костей или подбрасывания монет. Она имеет место везде, где существует несколько возможностей, и ни одну из них нельзя предпочесть другой. Если вы подбрасываете монету, она должна упасть или орлом, или решкой, но и то и другое представляется равновероятным. Следовательно, шансы у орла и решки равны 50%, единица принимается за достоверность. Сходным образом, если вы бросаете кость, она может упасть вверх любой из шести граней, и нет оснований для предпочтения одной из них, следовательно, шанс каждой равен 1/6. Такого рода вероятность используют в своей работе страховые кампании. Они не знают, какое именно здание сгорит, но знают, какой процент зданий сгорает ежегодно. Они не знают, как долго будет жить конкретный человек, но знают среднюю продолжительность жизни в любой данный период. Во всех подобных случаях оценка вероятности сама по себе не является просто вероятной, за исключением того смысла, в котором всё знание лишь вероятно. Оценка вероятности сама по себе может обладать высокой степенью вероятности. Иначе страховые кампании разорились бы.
Большие усилия были приложены для того, чтобы повысить вероятность индукции, но есть основания полагать, что все эти попытки были напрасны. Вероятность, характерная для индуктивных заключений, практически всегда носит, как я сказал выше, неопределённый характер.
Теперь я поясню, что это такое.
Стало тривиальным утверждение, что всё человеческое знание ошибочно. Очевидно то, что ошибки бывают разными. Если я скажу, что Будда жил в VI в. до Рождества Христова, вероятность ошибки будет очень велика. Если я скажу, что Цезарь был убит, вероятность ошибки будет мала.
Если я скажу, что сейчас идёт великая война, то вероятность ошибки столь мала, что её наличие может допустить лишь философ или логик. Эти примеры касаются исторических событий, но сходная градация существует и в отношении научных законов. Некоторые из них имеют явный характер гипотез, которым никто не придаст более серьезного статуса в виду отсутствия эмпирических данных в их пользу, в то время как другие представляются настолько определёнными, что со стороны учёных практически нет сомнений в их истинности. (Когда я говорю «истина», я имею в виду «приблизительная истина», поскольку каждый научный закон подвержен некоторым поправкам.)
Вероятность - это нечто находящееся между тем, в чем мы уверены, и тем, что мы более или менее склонны допустить, если это слово понимать в смысле математической теории вероятности.
Правильнее было бы говорить о степенях несомненности или о степенях надёжности . Это более широкая концепция того, что я назвал «определённой вероятностью», которая к тому же является и более важной».
Бертран Рассел, Искусство делать выводы / Искусство мыслить, М., «Дом интеллектуальной книги», 1999 г., с. 50-51.
Вряд ли многие люди задумываются, можно ли просчитать события, которые в той или иной мере случайны. Выражаясь простыми словами, реально ли узнать, какая сторона кубика в выпадет в следующий раз. Именно этим вопросом задались два великих ученых, положившие начало такой науке, как теория вероятности, вероятность события в которой изучается достаточно обширно.
Зарождение
Если попытаться дать определение такому понятию, как теория вероятности, то получится следующее: это один из разделов математики, который занимается изучением постоянства случайных событий. Ясное дело, данное понятие толком не раскрывает всю суть, поэтому необходимо рассмотреть ее более детально.
Хотелось бы начать с создателей теории. Как было выше упомянуто, их было двое, это и Именно они одни из первых попытались с использованием формул и математических вычислений просчитать исход того или иного события. В целом же зачатки этой науки проявлялись еще в средневековье. В то время разные мыслители и ученые пытались проанализировать азартные игры, такие как рулетка, кости и так далее, тем самым установить закономерность и процентное соотношение выпадения того или иного числа. Фундамент же был заложен в семнадцатом столетии именно вышеупомянутыми учеными.
Поначалу их труды нельзя было отнести к великим достижениям в этой области, ведь все, что они сделали, это были попросту эмпирические факты, а опыты ставились наглядно, без использования формул. Со временем получилось добиться больших результатов, которые появились вследствие наблюдения за бросанием костей. Именно этот инструмент помог вывести первые внятные формулы.
Единомышленники
Нельзя не упомянуть о таком человеке, как Христиан Гюйгенс, в процессе изучения темы, носящей название "теория вероятности" (вероятность события освещается именно в этой науке). Данная персона очень интересна. Он, так же как и представленные выше ученые, пытался в виде математических формул вывести закономерность случайных событий. Примечательно, что делал он это не совместно с Паскалем и Ферма, то есть все его труды никак не пересекались с этими умами. Гюйгенс вывел

Интересен тот факт, что его работа вышла задолго до результатов трудов первооткрывателей, а точнее, на двадцать лет раньше. Среди обозначенных понятий известнее всего стали:
- понятие вероятности как величины шанса;
- математическое ожидание для дискретных случаев;
- теоремы умножения и сложения вероятностей.
Также нельзя не вспомнить который тоже внес весомый вклад в изучении проблемы. Проводя свои, ни от кого не зависящие испытания, он сумел представить доказательство закона больших чисел. В свою очередь, ученые Пуассон и Лаплас, которые работали в начале девятнадцатого столетия, смогли доказать изначальные теоремы. Именно с этого момента для анализа ошибок в ходе наблюдений начали использовать теорию вероятностей. Стороной обойти данную науку не смогли и русские ученые, а точнее Марков, Чебышев и Дяпунов. Они, исходя из проделанной работы великих гениев, закрепили данный предмет в качестве раздела математики. Трудились эти деятели уже в конце девятнадцатого столетия, и благодаря их вкладу, были доказаны такие явления, как:
- закон больших чисел;
- теория цепей Маркова;
- центральная предельная теорема.
Итак, с историей зарождения науки и с основными персонами, повлиявшими на нее, все более или менее понятно. Сейчас же пришло время конкретизировать все факты.
Основные понятия
Перед тем как касаться законов и теорем, стоит изучить основные понятия теории вероятностей. Событие в ней занимает главенствующую роль. Данная тема довольно объемная, но без нее не удастся разобраться во всем остальном.

Событие в теории вероятности - этолюбая совокупность исходов проведенного опыта. Понятий данного явления существует не так мало. Так, ученый Лотман, работающий в этой области, высказался, что в данном случае речь идет о том, что «произошло, хотя могло и не произойти».
Случайные события (теория вероятности уделяет им особое внимание) - это понятие, которое подразумевает абсолютно любое явление, имеющее возможность произойти. Или же, наоборот, этот сценарий может не случиться при выполнении множества условий. Также стоит знать, что захватывают весь объем произошедших явлений именно случайные события. Теория вероятности указывает на то, что все условия могут повторяться постоянно. Именно их проведение получило название "опыт" или же "испытание".
Достоверное событие - это то явление, которое в данном испытании на сто процентов произойдет. Соответственно, невозможное событие - это то, которое не случится.
Совмещение пары действий (условно случай A и случай B) есть явление, которое происходит одновременно. Они обозначаются как AB.
Сумма пар событий А и В - это С, другими словами, если хотя бы одно из них произойдет (А или В), то получится С. Формула описываемого явления записывается так: С = А + В.
Несовместные события в теории вероятности подразумевают, что два случая взаимно исключают друг друга. Одновременно они ни в коем случае не могут произойти. Совместные события в теории вероятности - это их антипод. Здесь подразумевается, что если произошло А, то оно никак не препятствует В.
Противоположные события (теория вероятности рассматривает их очень подробно) просты для понимания. Лучше всего разобраться с ними в сравнении. Они почти такие же, как и несовместные события в теории вероятности. Но их отличие заключается в том, что одно из множества явлений в любом случае должно произойти.
Равновозможные события - это те действия, возможность повтора которых равна. Чтобы было понятней, можно представить бросание монеты: выпадение одной из ее сторон равновероятно выпадению другой.

Благоприятствующее событие легче рассмотреть на примере. Допустим, есть эпизод В и эпизод А. Первое - это бросок игрального кубика с появлением нечетного числа, а второе - появление числа пять на кубике. Тогда получается, что А благоприятствует В.
Независимые события в теории вероятности проецируются только на два и больше случаев и подразумевают независимость какого-либо действия от другого. Например, А - выпадение решки при бросании монеты, а В - доставание валета из колоды. Они и есть независимые события в теории вероятности. С этим моментом стало понятнее.
Зависимые события в теории вероятности также допустимы лишь для их множества. Они подразумевают зависимость одного от другого, то есть явление В может произойти только в том случае, если А уже произошло или же, наоборот, не произошло, когда это - главное условие для В.
Исход случайного эксперимента, состоящего из одного компонента, - это элементарные события. Теория вероятности поясняет, что это такое явление, которое совершилось лишь единожды.
Основные формулы
Итак, выше были рассмотрены понятия "событие", "теория вероятности", определение основным терминам этой науки также было дано. Сейчас же пришло время ознакомиться непосредственно с важными формулами. Эти выражения математически подтверждают все главные понятия в таком непростом предмете, как теория вероятности. Вероятность события и здесь играет огромную роль.
Начать лучше с основных И перед тем как приступить к ним, стоит рассмотреть, что это такое.

Комбинаторика - это в первую очередь раздел математики, он занимается изучением огромного количества целых чисел, а также различных перестановок как самих чисел, так и их элементов, различных данных и т. п., ведущих к появлению ряда комбинаций. Помимо теории вероятности, эта отрасль важна для статистики, компьютерной науки и криптографии.
Итак, теперь можно переходить к представлению самих формул и их определению.
Первой из них будет выражение для числа перестановок, выглядит оно следующим образом:
P_n = n ⋅ (n - 1) ⋅ (n - 2)…3 ⋅ 2 ⋅ 1 = n!
Применяется уравнение только в том случае, если элементы различаются лишь порядком расположения.
Теперь будет рассмотрена формула размещения, выглядит она так:
A_n^m = n ⋅ (n - 1) ⋅ (n-2) ⋅ ... ⋅ (n - m + 1) = n! : (n - m)!
Это выражение применимо уже не только лишь к порядку размещения элемента, но и к его составу.
Третье уравнение из комбинаторики, и оно же последнее, называется формулой для числа сочетаний:
C_n^m = n ! : ((n - m))! : m !
Сочетанием называются выборки, которые не упорядочены, соответственно, к ним и применяется данное правило.
С формулами комбинаторики получилось разобраться без труда, теперь можно перейти к классическому определению вероятностей. Выглядит это выражение следующим образом:
В данной формуле m - это число условий, благоприятствующих событию A, а n - число абсолютно всех равновозможных и элементарных исходов.
Существует большое количество выражений, в статье не будут рассмотрены все, но затронуты будут самые важные из них такие, как, например, вероятность суммы событий:
P(A + B) = P(A) + P(B) - эта теорема для сложения только несовместных событий;
P(A + B) = P(A) + P(B) - P(AB) - а эта для сложения только совместимых.

Вероятность произведения событий:
P(A ⋅ B) = P(A) ⋅ P(B) - эта теорема для независимых событий;
(P(A ⋅ B) = P(A) ⋅ P(B∣A); P(A ⋅ B) = P(A) ⋅ P(A∣B)) - а эта для зависимых.
Закончит список формула событий. Теория вероятностей рассказывает нам о теоремеБайеса, которая выглядит так:
P(H_m∣A) = (P(H_m)P(A∣H_m)) : (∑_(k=1)^n P(H_k)P(A∣H_k)),m = 1,...,n
В данной формуле H 1 , H 2 , …, H n - это полная группа гипотез.
Примеры
Если тщательно изучить любой раздел математики, в нем не обходится без упражнений и образцов решений. Так и теория вероятности: события, примеры здесь являются неотъемлемым компонентом, подтверждающим научные выкладки.
Формула для числа перестановок
Допустим, в карточной колоде есть тридцать карт, начиная с номинала один. Далее вопрос. Сколько есть способов сложить колоду так, чтобы карты с номиналом один и два не были расположены рядом?
Задача поставлена, теперь давайте перейдем к ее решению. Для начала нужно определить число перестановок из тридцати элементов, для этого берем представленную выше формулу, получается P_30 = 30!.
Исходя из этого правила, мы узнаем, сколько есть вариантов сложить колоду по-разному, но нам необходимо вычесть из них те, в которых первая и вторая карта будут рядом. Для этого начнем с варианта, когда первая находится над второй. Получается, что первая карта может занять двадцать девять мест - с первого по двадцать девятое, а вторая карта со второго по тридцатое, получается всего двадцать девять мест для пары карт. В свою очередь, остальные могут принимать двадцать восемь мест, причем в произвольном порядке. То есть для перестановки двадцати восьми карт есть двадцать восемь вариантов P_28 = 28!
В итоге получается, что если рассматривать решение, когда первая карта находится над второй, лишних возможностей получится 29 ⋅ 28! = 29!

Используя этот же метод, нужно вычислить число избыточных вариантов для того случая, когда первая карта находится под второй. Получается также 29 ⋅ 28! = 29!
Из этого следует, что лишних вариантов 2 ⋅ 29!, в то время как необходимых способов сбора колоды 30! - 2 ⋅ 29!. Остается только лишь посчитать.
30! = 29! ⋅ 30; 30!- 2 ⋅ 29! = 29! ⋅ (30 - 2) = 29! ⋅ 28
Теперь нужно перемножать между собой все числа от одного до двадцати девяти, после чего в конце умножить все на 28. Ответ получается 2,4757335 ⋅〖10〗^32
Решение примера. Формула для числа размещения
В данной задаче необходимо выяснить, сколько есть способов, чтобы поставить пятнадцать томов на одной полке, но при условии, что всего томов тридцать.
В этой задаче решение немного проще, чем в предыдущей. Используя уже известную формулу, необходимо вычислить суммарное число расположений из тридцати томов по пятнадцать.
A_30^15 = 30 ⋅ 29 ⋅ 28⋅... ⋅ (30 - 15 + 1) = 30 ⋅ 29 ⋅ 28 ⋅ ... ⋅ 16 = 202 843 204 931 727 360 000
Ответ, соответственно, будет равен 202 843 204 931 727 360 000.
Теперь возьмем задачу чуть сложнее. Необходимо узнать, сколько есть способов расставить тридцать книг на двух книжных полках, при условии, что на одной полке могут находиться лишь пятнадцать томов.
Перед началом решения хотелось бы уточнить, что некоторые задачи решаются несколькими путями, так и в этой есть два способа, но в обоих применена одна и та же формула.
В этой задаче можно взять ответ из предыдущей, ведь там мы вычислили, сколько раз можно заполнить полку на пятнадцать книг по-разному. Получилось A_30^15 = 30 ⋅ 29 ⋅ 28 ⋅ ... ⋅ (30 - 15 + 1) = 30 ⋅ 29 ⋅ 28 ⋅ ...⋅ 16.
Вторую же полку рассчитаем по формуле перестановки, ведь в нее помещается пятнадцать книг, в то время как всего остается пятнадцать. Используем формулу P_15 = 15!.
Получается, что в сумме будет A_30^15 ⋅ P_15 способов, но, помимо этого, произведение всех чисел от тридцати до шестнадцати надо будет умножить на произведение чисел от одного до пятнадцати, в итоге получится произведение всех чисел от одного до тридцати, то есть ответ равен 30!
Но эту задачу можно решить и по-иному - проще. Для этого можно представить, что есть одна полка на тридцать книг. Все они расставлены на этой плоскости, но так как условие требует, чтобы полок было две, то мы одну длинную пилим пополам, получается две по пятнадцать. Из этого получается что вариантов расстановки может быть P_30 = 30!.
Решение примера. Формула для числа сочетания
Сейчас будет рассмотрен вариант третьей задачи из комбинаторики. Необходимо узнать, сколько способов есть, чтобы расставить пятнадцать книг при условии, что выбирать необходимо из тридцати абсолютно одинаковых.
Для решения будет, конечно же, применена формула для числа сочетаний. Из условия становится понятным, что порядок одинаковых пятнадцати книг не важен. Поэтому изначально нужно выяснить общее число сочетаний из тридцати книг по пятнадцать.
C_30^15 = 30 ! : ((30-15)) ! : 15 ! = 155 117 520
Вот и все. Используя данную формулу, в кратчайшее время удалось решить такую задачу, ответ, соответственно, равен 155 117 520.
Решение примера. Классическое определение вероятности
С помощью формулы, указанной выше, можно найти ответ в несложной задаче. Но это поможет наглядно увидеть и проследить ход действий.
В задаче дано, что в урне есть десять абсолютно одинаковых шариков. Из них четыре желтых и шесть синих. Из урны берется один шарик. Необходимо узнать вероятность доставания синего.
Для решения задачи необходимо обозначить доставание синего шарика событием А. Данный опыт может иметь десять исходов, которые, в свою очередь, элементарные и равновозможные. В то же время из десяти шесть являются благоприятствующими событию А. Решаем по формуле:
P(A) = 6: 10 = 0,6
Применив эту формулу, мы узнали, что возможность доставания синего шарика равна 0,6.
Решение примера. Вероятность суммы событий
Сейчас будет представлен вариант, который решается с использованием формулы вероятности суммы событий. Итак, в условии дано, что есть два ящика, в первом находится один серый и пять белых шариков, а во втором - восемь серых и четыре белых шара. В итоге из первого и второго короба взяли по одному из них. Необходимо узнать, каков шанс того, что доставаемые шарики будут серого и белого цвета.
Чтобы решить данную задачу, необходимо обозначить события.
- Итак, А - взяли серый шарик из первого ящика: P(A) = 1/6.
- А’ - взяли белый шарик также из первого ящика: P(A") = 5/6.
- В - извлекли серый шарик уже из второго короба: P(B) = 2/3.
- В’ - взяли серый шарик из второго ящика: P(B") = 1/3.
По условию задачи необходимо, чтобы случилось одно из явлений: АВ’ или же А’В. Используя формулу, получаем: P(AB") = 1/18, P(A"B) = 10/18.
Сейчас была использована формула по умножению вероятности. Далее, чтобы узнать ответ, необходимо применить уравнение их сложения:
P = P(AB" + A"B) = P(AB") + P(A"B) = 11/18.
Вот так, используя формулу, можно решать подобные задачи.
Итог
В статье была представлена информация по теме "Теория вероятности", вероятность события в которой играет важнейшую роль. Конечно же, не все было учтено, но, исходя из представленного текста, можно теоретически ознакомиться с данным разделом математики. Рассматриваемая наука может пригодиться не только в профессиональном деле, но и в повседневной жизни. С ее помощью можно просчитать любую возможность какого-либо события.
В тексте были затронуты также знаменательные даты в истории становления теории вероятности как науки, и фамилии людей, чьи труды были в нее вложены. Вот так человеческое любопытство привело к тому, что люди научились просчитывать даже случайные события. Когда-то они просто заинтересовались этим, а сегодня об этом уже знают все. И никто не скажет, что ждет нас в будущем, какие еще гениальные открытия, связанные с рассматриваемой теорией, будут совершены. Но одно можно сказать точно - исследования на месте не стоят!
Чтобы количественно сравнивать между собой события по степени их возможности, очевидно, нужно с каждым событием связать определённое число, которое тем больше, чем более возможно событие. Такое число мы назовём вероятностью события. Таким образом, вероятность события есть численная мера степени объективной возможности этого события.
Первым по времени определением вероятности следует считать классическое, которое возникло из анализа азартных игр и применялось вначале интуитивно.
Классический способ определения вероятности основан на понятии равновозможных и несовместных событий, которые являются исходами данного опыта и образуют полную группу несовместных событий.
Наиболее простым примером равновозможных и несовместных событий, образующих полную группу, является появление того или иного шара из урны, содержащей несколько одинаковых по размеру, весу и другим осязаемым признакам шаров, отличающихся лишь цветом, тщательно перемешанных перед выниманием.
Поэтому об испытании, исходы которого образуют полную группу несовместных и равновозможных событий, говорят, что оно сводится к схеме урн, или схеме случаев , или укладывается в классическую схему.
Равновозможные и несовместные события, составляющие полную группу, будем называть просто случаями или шансами. При этом в каждом опыте наряду со случаями могут происходить и более сложные события.
Пример : При подбрасывании игральной кости наряду со случаями А i - выпадение i- очков на верхней грани можно рассматривать такие события, как В - выпадение чётного числа очков, С - выпадение числа очков, кратных трём …
По отношению к каждому событию, которое может произойти при осуществлении эксперимента, случаи делятся на благоприятствующие , при которых это событие происходит, и неблагоприятствующие, при которых событие не происходит. В предыдущем примере, событию В благоприятствуют случаи А 2 , А 4 , А 6 ; событию С - случаи А 3 , А 6 .
Классической вероятностью появления некоторого события называется отношение числа случаев, благоприятствующих появлению этого события, к общему числу случаев равновозможных, несовместных, составляющих полную группу в данном опыте:
где Р(А) - вероятность появления события А; m - число случаев, благоприятствующих событию А; n - общее число случаев.
Примеры:
1) (смотри пример выше) Р(В) = , Р(С) = .
2) В урне находятся 9 красных и 6 синих шаров. Найти вероятность того, что вынутые наугад один, два шара окажутся красными.
А - вынутый наугад шар красный:
m = 9, n = 9 + 6 = 15, P(A) =
B - вынутые наугад два шара красные:

Из классического определения вероятности вытекают следующие свойства (показать самостоятельно):
1) Вероятность невозможного события равна 0;
2) Вероятность достоверного события равна 1;
3) Вероятность любого события заключена между 0 и 1;
4) Вероятность события, противоположного событию А,
![]()
Классическое определение вероятности предполагает, что число исходов испытания конечно. На практике же весьма часто встречаются испытания, число возможных случаев которых бесконечно. Кроме того, слабая сторона классического определения состоит в том, что очень часто невозможно представить результат испытания в виде совокупности элементарных событий. Ещё труднее указать основания, позволяющие считать элементарные исходы испытания равновозможными. Обычно о равновозможности элементарных исходов испытания заключают из соображений симметрии. Однако такие задачи на практике встречаются весьма редко. По этим причинам наряду с классическим определением вероятности пользуются и другими определениями вероятности.
Статистической вероятностью события А называется относительная частота появления этого события в произведённых испытаниях:
![]()
где - вероятность появления события А;
Относительная частота появления события А;
Число испытаний, в которых появилось событие А;
Общее число испытаний.
В отличие от классической вероятности статистическая вероятность является характеристикой опытной, экспериментальной.
Пример : Для контроля качества изделий из партии наугад выбрано 100 изделий, среди которых 3 изделия оказались бракованными. Определить вероятность брака.
![]() .
.
Статистический способ определения вероятности применим лишь к тем событиям, которые обладают следующими свойствами:
Рассматриваемые события должны быть исходами только тех испытаний, которые могут быть воспроизведены неограниченное число раз при одном и том же комплексе условий.
События должны обладать статистической устойчивостью (или устойчи- востью относительных частот). Это означает, что в различных сериях испытаний относительная частота события изменяется незначительно.
Число испытаний, в результате которых появляется событие А, должно быть достаточно велико.
Легко проверить, что свойства вероятности, вытекающие из классического определения, сохраняются и при статистическом определении вероятности.
вероятность (probability) - число от 0 до 1, которое отражает шансы того, что случайное событие произойдет, где 0 - это полное отсутствие вероятности происхождения события, а 1 означает, что рассматриваемое событие определенно произойдет.
Вероятность события E является числом от до 1.
Сумма вероятностей взаимоисключающих событий равна 1.
эмпирическая вероятность - вероятность, которая посчитана как относительная частота события в прошлом, извлеченная из анализа исторических данных.
Вероятность очень редких событий нельзя посчитать эмпирически.
субъективная вероятность - вероятность, основанная на личной субъективной оценке события безотносительно исторических данных. Инвесторы, которые принимают решения о покупке и продаже акций зачастую действуют именно исходя из соображений субъективной вероятности.
априорная вероятность -
Шанс 1 из… (odds) того что событие произойдет через понятие вероятности. Шанс появления события выражается через вероятность так: P/(1-P).
Например, если вероятность события 0,5, то шанс события 1 из 2 т.к. 0,5/(1-0,5).
Шанс того, что событие не произойдет вычисляется по формуле (1-P)/P
Несогласованная вероятноть - например в цене акций компании А на 85% учтено возможное событие E, а в цене акций компании Б всего на 50%. Это называется несогласованная вероятность. Согласно теореме голландских ставок, несогласованная вероятность создает возможности для извлечения прибыли.
Безусловная вероятность - это ответ на вопрос «Какова вероятность того, что событие произойдет?»
Условная вероятность - это ответ на вопрос: «Какова вероятность события A если событие Б произошло». Условная вероятность обозначается как P(A|B).
Совместная вероятность - вероятность того, что события А и Б произойдут одновременно. Обозначается как P(AB).
P(A|B) = P(AB)/P(B) (1)
P(AB) = P(A|B)*P(B)
Правило суммирования вероятностей:
Вероятность того, что случится либо событие A либо событие B -
P (A or B) = P(A) + P(B) - P(AB) (2)
Если события A и B взаимоисключающие, то
P (A or B) = P(A) + P(B)
Независимые события - события A и B независимы если
P(A|B) = P(A), P(B|A) = P(B)
То есть это последовательность результатов, где значение вероятности постоянно от одного собятия к другому.
Бросок монеты - пример такого события, - результат каждого следующего броска не зависит от результата предыдущего.
Зависимые события - это такие события, когда вероятность появления одного зависит от вероятности появления другого.
Правило умножения вероятностей независимых событий:
Если события A и B независимы, то
P(AB) = P(A) * P(B) (3)
Правило полной вероятности:
P(A) = P(AS) + P(AS") = P(A|S")P(S) + P (A|S")P(S") (4)
S и S" - взаимоисключающие события
математическое ожидание (expected value) случайной переменной есть среднее возможных исходов случайной величины. Для события X матожидание обоначается как E(X).
Допустим у нас есть 5 значений взаимоисключающих событий c определенной вероятностью (например доход компании составил такую-то сумму с такой вероятностью). Матожиданием будет сумма всех исходов помноженных на их вероятность:
Дисперсия случайной величины - матожидание квадратных отклонений случайной величины от ее матожидания:
s 2 = E{ 2 } (6)
Условное матожидание (conditional expected value) - матожидание случайной величины X при условии того, что событие S уже произошло.